2016の不思議（2016になる数式)

みなさん、こんにちは

インターネット上で、2016になる数式になるまとめサイトを発見しました。

世の中にはすごい人がぎょうさんおるんやなーと感動していたのですが、せっかくなのでセンター問題風にアレンジしてみました。

IAの整数とⅡBの数列が混在していますが、興味のある人やシグマが心配という人は、ぜひチャレンジしてみてください。時間のない人も上のまとめサイトはサクッとみて記憶しておいたほうが良いと思いますよ！

では、このあと問題です(問題はクリックすると大きな画像になります)。

では、さっそく解答です。

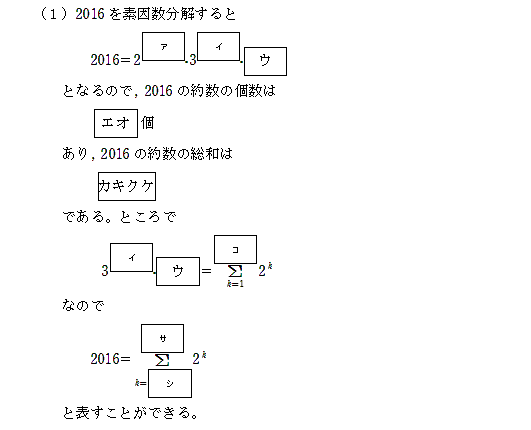
（１）2016を素因数分解すると
$\hspace*{20pt}2016=2^5 \cdot 3^2 \cdot 7$
約数に含まれる素因数は2が0～5個の6パターン, 3が0～2個の3パターン,7が0～1個の2パターン考えられるので, 正の約数の個数は
$\hspace*{20pt}6 \cdot 3 \cdot 2=36$
正の約数の総和は
$\hspace*{20pt}(2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5) \cdot (3^0 + 3^1 + 3^2) \cdot (7^0 + 7^1)$
$\hspace*{20pt}=2^0 \cdot \frac{2^6-1}{2-1} \cdot 3^0 \cdot \frac{3^3-1}{3-1} \cdot 8$
$\hspace*{20pt}=63 \cdot 13 \cdot 8$
$\hspace*{20pt}=6552$
となる。ところで
$\hspace*{20pt}3^2 \cdot 7 =63=2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5$
$\hspace*{20pt}=\displaystyle{ \sum_{k=0}^{5} 2^k }$
なので
$\hspace*{20pt}2016=2^5 \cdot(2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5)$
$\hspace*{20pt}=2^5 + 2^6 + 2^7 + 2^8 + 2^9 + 2^{10}$
$\hspace*{20pt}=\displaystyle{ \sum_{k=5}^{10} 2^k }$
【答】(アイウ) 5,2,7 (エオ) 36 (カキクケ) 6552 (コ) 5 (サシス)10,5

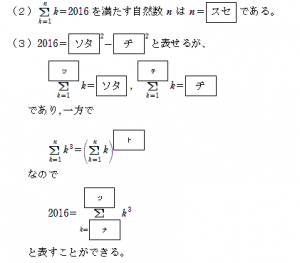
(2)
$\hspace*{20pt}\displaystyle{ \sum_{k=1}^{n} k } = \frac{1}{2}n(n + 1)$
なので, (1) の結果とから
$\hspace*{20pt}n(n + 1) =2^6 \cdot 3^2 \cdot 7$
と変形できるが, 左辺は奇数と偶数の積であることに着目すると2の6乗はnかn+1のどちらかの因数であり
$\hspace*{20pt}n(n + 1) =64 \cdot 63$
と変形できる。nは自然数なので
$\hspace*{20pt}n = 63$
【答】(セソ) 63
（３）空欄タチ,空欄ツに入る数字はシグマ計算の結果得られる数でもあるから,ツの候補は1,3,6しかないが,1,6 の場合は空欄タチに当てはまる数値は得られず
$\hspace*{20pt}2016=2025-9=45^2-3^2$
と表せるが
$\hspace*{20pt}45=1 + 2 + \cdots + 9 = \displaystyle{ \sum_{k=1}^{9} k } , \hspace*{20pt}3=1 + 2 = \displaystyle{ \sum_{k=1}^{2} k }$
と変形できる。一方で
$\hspace*{20pt}\displaystyle{ \sum_{k=1}^{n} k^3 } = \{ \frac{1}{2}n(n + 1) \} ^2 = \displaystyle(\sum_{k=1}^{n} k )^2$
なので
$\hspace*{20pt}2016=\displaystyle(\sum_{k=1}^{9} k )^2 -\displaystyle(\sum_{k=1}^{2} k )^2$
$\hspace*{20pt}=\displaystyle{\sum_{k=1}^{9} k^3 } -\displaystyle{\sum_{k=1}^{2} k^3$
$\hspace*{20pt}=\displaystyle{\sum_{k=3}^{9} k^3$
【答】(タチ) 45 (ツ) 3 (テ) 9 (ト) 2 (ナ) 2 (ニ) 3