2桁×2桁の計算のうち、ある特別な場合はインド式掛け算を使うと一瞬で計算ができます。
インド式掛け算
代表的な例を計算してみると
インド式掛け算
どんな場合に?
計算のやりかたは?
例題
\begin{eqnarray} (1) \ 34 \times 36 &=& (3 \times 4) \times 100 + 4 \times 6 \hspace{5mm} \cdots \mbox{①} \\ &=& 1224 \hspace{5mm} \cdots (\mbox{答}) \\ (2) \ 43 \times 63 &=& (4 \times 6 +3) \times 100 + 3 \times 3 \hspace{5mm} \cdots \mbox{②} \\ &=& 2709 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}となりますが、①や②の変形がなぜ可能なのかを紐解き、同じように計算できるパターンが他にもないか深堀りしていきましょう。
十の位と一の位にわけて、長方形の面積を考えてみるとほぼ解決してしまうのですが…。
例題
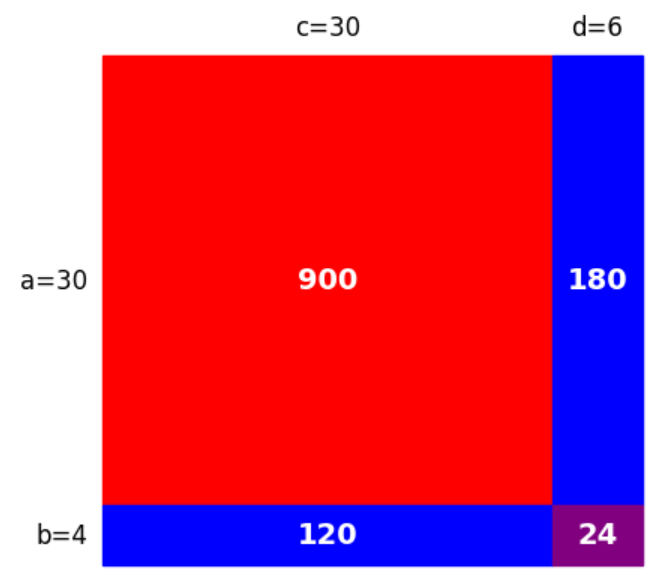
\begin{eqnarray} (1) \ 34 \times 36 &=& (30+4) \times (30+6) \\ &=& 30 \times 30 + \color{yellow}{30} \times \color{red}{6} + \color{red}{4} \times \color{yellow}{30} +4 \times 6 \\ &=& 30 \times 30 + \color{yellow}{30} \times (\color{red}{6} + \color{red}{4}) +4 \times 6 \\ &=& 30 \times 30 + \color{yellow}{30} \times \color{red}{10} +4 \times 6 \\ &=& 30 \times ( 30 + 10 ) +4 \times 6 \hspace{5mm} \cdots \mbox{①’}\\ &=& 1224 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}長方形の面積を考えると、右上と左下に現れる青色部分の合計が簡単な数値になることがお分かりいただけるのではないでしょうか?
では (2) ではどのようになるのでしょうか?十の位と一の位に分けて考えてみましょう。
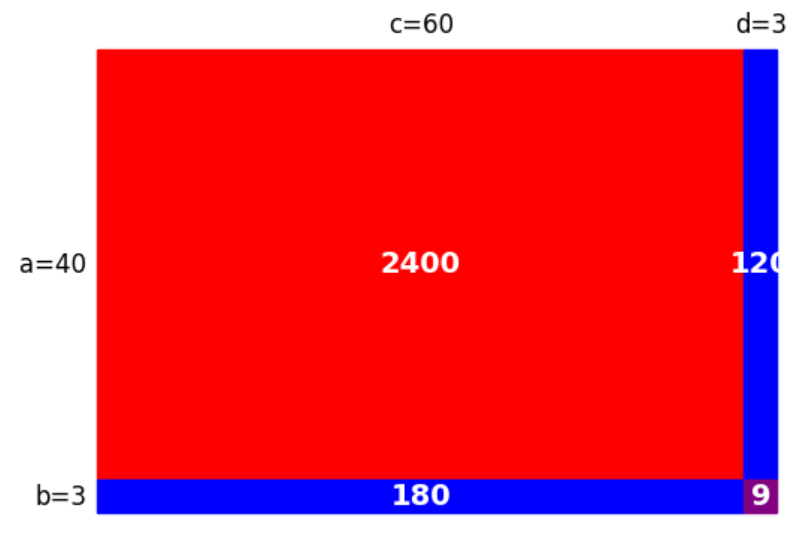
\begin{eqnarray} (2) \ 43 \times 63 &=& (40+3) \times (60+3) \\ &=& 40 \times 60 + \color{red}{40} \times \color{yellow}{3} + \color{yellow}{3} \times \color{red}{60} +3 \times 3 \\ &=& 40 \times 60 + \color{yellow}{3} \times (\color{red}{40} + \color{red}{60} ) +3 \times 3 \\ &=& 40 \times 60 + \color{yellow}{3} \times \color{red}{100} +3 \times 3 \hspace{5mm} \cdots \mbox{②’} \\ &=& 2709 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}こういった計算が出来るのは、どんな場合があるのでしょうか。
インド式掛け算ができるかどうかのチェックポイント
(a) 同じ数字がある
(b) 和が10になる
ただ、この条件だと $33 \times 46 $ も含まれてしまいますが、実はこのパターンも全く同じように計算できます。
例題
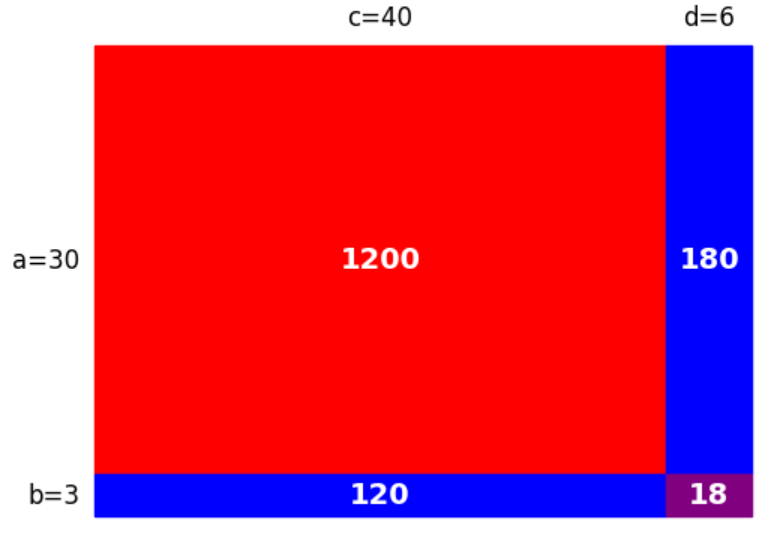
\begin{eqnarray} (3) \ 33 \times 46 &=& (30+3) \times (40+6) \\ &=& 30 \times 40 + \color{yellow}{30} \times \color{red}{6} + \color{yellow}{3} \times \color{red}{4}\color{yellow}{0} +3 \times 6 \\ &=& 30 \times 40 + \color{yellow}{30} \times (\color{red}{6} + \color{red}{4}) +3 \times 6 \\ &=& 30 \times 40 + \color{yellow}{30} \times \color{red}{10} +3 \times 6 \\ &=& 1518 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}同じように計算できるパターンは、まだ存在します。
和が5でも、同じ数字が偶数ならばほとんど計算方法は変わりません。
例題
\begin{eqnarray} (4) \ 43 \times 42 &=& (40+3) \times (40+2) \\ &=& 40 \times 40 + \color{yellow}{40} \times \color{red}{3} + \color{red}{2} \times \color{yellow}{40} +3 \times 2 \\ &=& 40 \times 40 + \color{yellow}{40} \times (\color{red}{3} + \color{red}{2}) +3 \times 2 \\ &=& 40 \times 40 + \color{yellow}{40} \times \color{red}{5} +3 \times 2 \\ &=& 1806 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}最後に、計算の仕方をまとめておきましょう。
インド式掛け算ができるかどうかのチェックポイント
(a) 同じ数字がある
(b) 和が10になる
(c) 和が5や15でも、同じ数字が偶数である
インド式掛け算のやりかた
(a) チェックポイントをクリアしたら、十の位同士を掛ける
(b) 繰り上がってくる数字を(a)に加えて、百の位まで計算する
(c) 最後に一の位同士を掛けて (b)までの結果に加える
最後に練習問題を追加しておきます。
練習問題
\[(1) \ 61 \times 69 \] \[(2) \ 83 \times 23 \] \[(3) \ 77 \times 46 \] \[(4) \ 66 \times 78 \]練習問題の回答です。
練習問題解答
\begin{eqnarray} (1) \ 61 \times 69 &=& (6 \times 7) \times 100 + 9 \\ &=& 4209 \hspace{5mm} \cdots (\mbox{答}) \\ (2) \ 83 \times 23 &=& (8 \times 2 +3) \times 100 +9 \\ &=& 1909 \hspace{5mm} \cdots (\mbox{答}) \\ (3) \ 77 \times 46 &=& (7 \times 5) \times 100+42 \\ &=& 3542 \hspace{5mm} \cdots (\mbox{答}) \\ (4) \ 66 \times 78 &=& (6 \times 7+ 9) + 48 \\ &=& 5148 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}YouTubeはこちら
YouTube動画でも解説していますので、よろしければご活用ください。

コメント