「余弦定理を立てたんだけど、そのあとの計算ができない」「75 $ ^{\circ} $ とか出てきたときに数Ⅱの加法定理を使わない方法はないかなぁ」と考えたり、悩んだりすることありませんか?
きょうは、余弦定理の立て方によってハマってしまうことがある問題を通して、余弦定理の立て方と特殊な角である15°、75°などが与えられたときに見通し良く問題を解いていく方法について学んでいきます。
問題はこちらです。
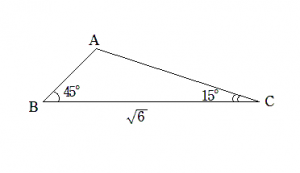
【問】\(
\triangle ABC
\) において, \(
BC= \sqrt{6}, \) \(
\angle B = 45^{\circ}, \) \(
\angle C = 15^{\circ}
\) のとき
(1)\(
AC
\) の長さを求めよ。
(2)\(
AB
\) の長さを求めよ。
【方針1】計算で押す
最初は、余弦定理や正弦定理を当てはめて、計算してみます。もちろん、この方法もできなければなりません。
(1)解答
(1) \(
\angle A = 180^{\circ}-(45^{\circ}+15^{\circ}) = 120^{\circ}
\) なので, 正弦定理より
\[
\frac{AC}{\sin 45^{\circ}} = \frac{\sqrt{6}}{\sin 120^{\circ}}
\]
分母を払って
\begin{align*}
AC\sin 120^{\circ} &= \sqrt{6}\sin 45^{\circ}\\
\frac{\sqrt{3}}{2}AC &= \sqrt{6} \cdot \frac{\sqrt{2}}{2}\\
AC &= 2
\end{align*}
このあと、\( AB=x \) などと置いて、\( \angle B \) を使って、余弦定理を使うとアレレ?という状況になる可能性がある。
「アレレ?」となる(2)の解答
$ \angle B $ を中心に余弦定理を立てると、答らしきものが2つ出てきてしまいます。
(2)余弦定理より
\[ AC^2=AB^2+BC^2-2AB \cdot BC \cos B \]
\( AB=x \) とし、与えられた数値も代入すると
\begin{align*}
2^2 &=x^2+\sqrt{6}^2-2x \cdot \sqrt{6} \cos 45^{\circ} \\
4 &=x^2+6-2x \cdot \sqrt{6} \cdot \frac{1}{\sqrt{2}} \\
\end{align*}
整理すると
\begin{align*}
x^2 -2\sqrt{3} x +2 &=0
\end{align*}
これを解くと
\begin{align*}
x=\sqrt{3} \pm \sqrt{\sqrt{3}^2-1 \cdot 2} = \sqrt{3} \pm 1
\end{align*}
どっちもプラスなので、答は2つあるの?
\( \sin \) は \( 0^{\circ} \) から \( 90^{\circ} \) まで増加関数であることを使うと搾りこめるので、その路線で解答を続けると
ここで、正弦定理より
\begin{align*}
\frac{AB}{\sin C}=&\frac{AC}{\sin B} \\
\frac{AB}{\sin 15^{\circ}}=&\frac{2}{\sin 45^{\circ}} \\
\end{align*}
となるが、$ \sin 15^{\circ} < \sin 45^{\circ} $ なので、 \[ AB<2 \] よって \[ AB=x=\sqrt{3}-1 \]
「アレレ?」の原因は・・・
では、なぜ「アレレ?」となってしまったのか。
実は $ 45^{\circ} $ と $2 $ と $ \sqrt{6} $ でできる三角形が、下図のように、もう一つ存在するからです。
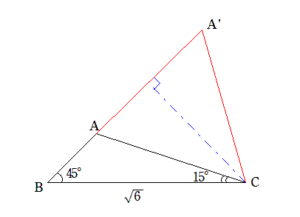
こうならないためには、余弦定理を立てるときに $120^{\circ} $である$ \angle A $ を中心にすると上手くいきます。
(2)解答【$\angle A $ を中心に余弦定理を立てる】
余弦定理より\[ BC^2=CA^2+AB^2-2CA \cdot AB \cos A \]
\( AB=x \) とし、与えられた数値も代入すると
\begin{align*}
\sqrt{6}^2 &= 2^2+x^2-2 \cdot 2 \cdot x \cos 120^{\circ} \\
6 &= 4+x^2-2 \cdot 2 \cdot x (-\frac{1}{2}) \\
2 &= x^2 + 2x \\
| x+1 | &= \sqrt{3}
\end{align*}
$x>0$より
\[ x=AB=\sqrt{3}-1 \]
【方針2】三角定規型三角形を組み合わせて、15°などを作る
背中合わせに三角形を組み合わせると
三角形の組み合わせかたは、下の2パターンがあります。
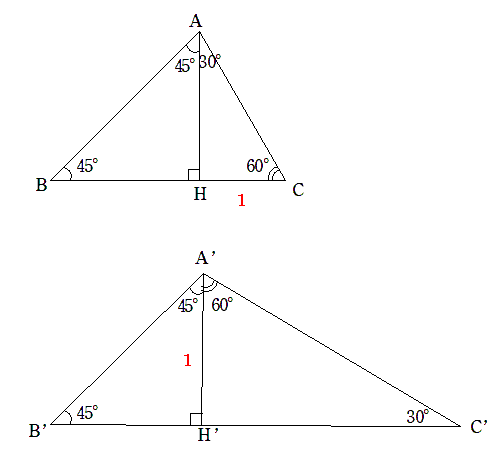
それぞれ、CH=1, A’H'(=B’H’)=1 とおくとすべての辺の長さが下図のように決まります。

これによって、75°や105°を含んだ計算が見通し良くできます。
折り返すと15°が現れる
AHやA’H’に関して一方の三角形を折り返すと15°が現れます。
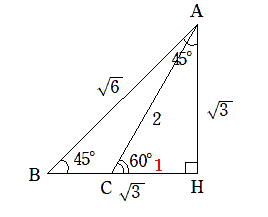
∠BAC=15°となり、この角を中心にしてAB,BC,CAの3辺の長さを使って余弦定理を立てることもできるし、∠B,AC,BCを使って正弦定理を立てることもできます。
この問題も、この図が描けると一瞬で答がわかります。
図形的解答
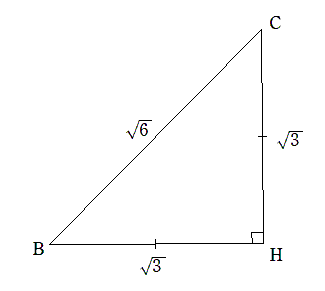
$BH=CH=\sqrt3, BC=\sqrt6 $ となる直角三角形を考える。
ここで、線分BH上にAH=1となるように点Aをとると
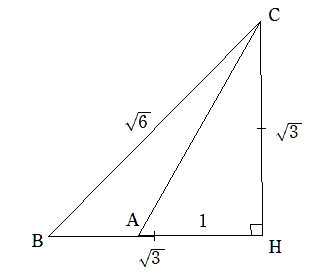
三角形AHCは、∠A=60°、∠C=30°の直角三角形となり、このとき∠ACB=15°。
これらから、AC=2、AB=$ \sqrt3 -1 $である。
【まとめ】三角定規型三角形を活用しよう
図形問題では、相似な三角形や直角三角形に着目できると道が拓けることが多いですが、直角三角形の中でも三角定規型に着目できると、簡単に答が見つかることも少なくありません。
着目すべきは、角度の$ 15(=45-30)
^{\circ} , 75(=45+30)
^{\circ} , 105(=60+45)
^{\circ} $ と辺の長さの $\sqrt3 \pm 1 $ です。辺はプラスマイナスの前後の比が$ \sqrt3 : 1$であればよいので、$\sqrt3 +3$ や $\sqrt 6- \sqrt 2 $などでも使える可能性がありますよ。
三角定規をくっつけて2つ描いて、練習してみてください。

コメント