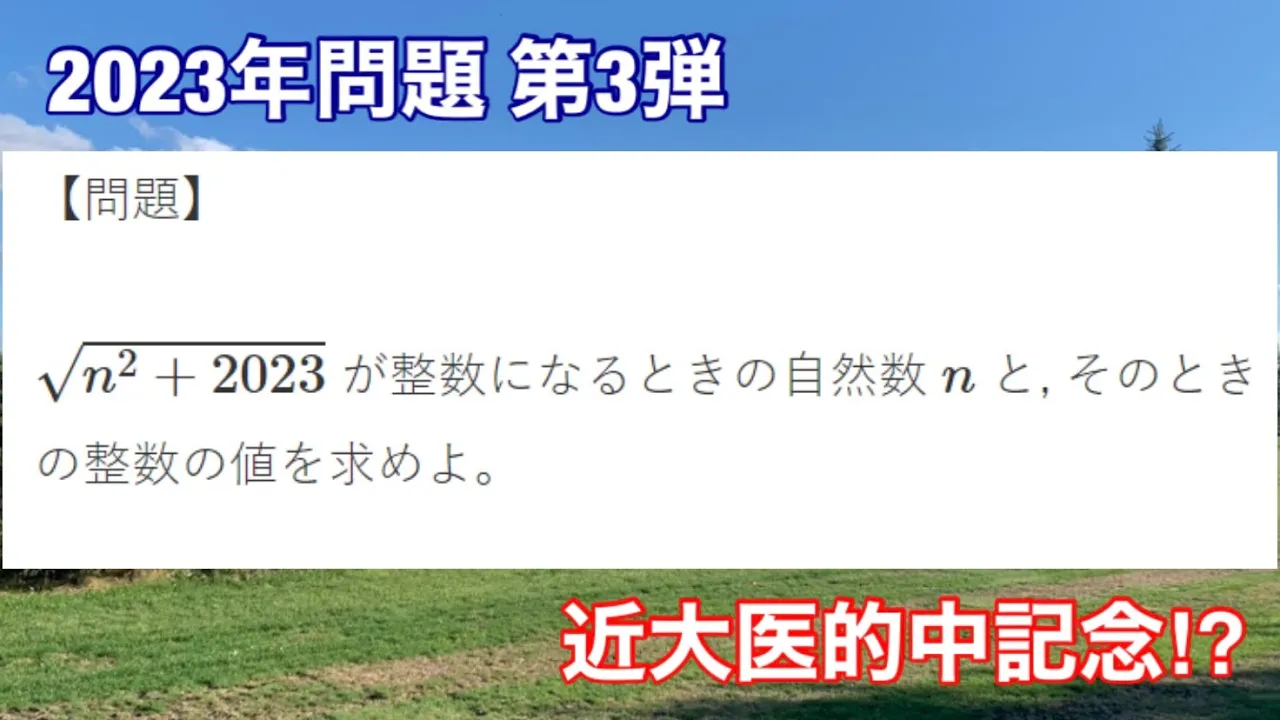
問題
$ \sqrt{n^2+2023} $ が整数になるときの自然数 $n$ と, そのときの整数の値を求めよ。
数学のコツ壺
・整数問題は、まず(整数)×(整数)の形に因数分解してみる
結局ポイントになりそうなのは、$2023=7 \cdot 17^2$とすぐに素因数分解できるかになりそうな気がします。
YouTube解説
YouTubeではより詳しく解説していますので、お時間のある時によろしければ御覧ください。
解答
$ \sqrt{n^2+2023} =k \hspace{2mm} (k\mbox{は自然数}) $ とおくと, 両辺$>0$なので
\begin{eqnarray}
n^2+2023 &=&k^2 \\
k^2-n^2&=& 2023 \\
(k-n)(k+n) &=& 7 \cdot 17^2
\end{eqnarray}
$k-n <k+n$ なので, $k-n$と$k+n$の組は
\begin{array}{c||c|c|c} \hline k-n&1&7&17\\ \hline k+n&7 \cdot 17^2 &17^2&7 \cdot 17\\ \hline \end{array}
これらより $k$と$n$の組は
\begin{array}{c||c|c|c} \hline k&1012&148&68\\ \hline n&1011 &141&51\\ \hline \end{array}
以上より
\[ n=1011 \mbox{のとき} 1012, \hspace{3mm} n=141 \mbox{のとき} 148, \hspace{3mm} n=51 \mbox{のとき} 68 \hspace{5mm} \cdots (\mbox{答})\]

コメント