今回は3文字の3乗の因数分解に関連した問題です。
問題
$ f(p, \ q, \ r) = p^3- q^3-27r^3- 9pqr $ について，次の問いに答えよ。
(1) $ f(p, \ q, \ r) $を因数分解せよ。
(2) 等式 $f(p, \ q, \ r) =0 $ と $ p^2- 10q – 30r = 11 $ との両方を満たす正の整数の組 $ (p, \ q, \ r) $ をすべて求めよ。
数学のコツ壺
・$ x^3+y^3+z^3-3xyz =(x+y+z)(x^2+y^2+z^2-xy-yz-zx) $ を覚えるだけなんてもったいなさすぎる！笑
対称式の変形、対称性を尊重するか崩して1文字に着目するか、そして、相加相乗平均にもつながります。
この公式だけでいろんなことが学べ過ぎるので、解答を先に記載します。
$ x^2+y^2+z^2-xy-yz-zx \geqq 0 $ を知っていれば、(2) もより短時間で解けます。
解答
（１）$ p=x, \ -q=y, \ -3r=z $ とすると
\begin{eqnarray}
f(p, \ q, \ r) &=& x^3+y^3+z^3-3xyz \\
&=& (x+y+z)(x^2+y^2+z^2-xy-yz-zx) \\
&=& (p-q-3r) \left\{ p^2+(-q)^2+(-3z)^2-p \cdot (-q)-(-q) \cdot (-3r)- (-3r) \cdot p \right\} \\
&=& (p-q-3r)(p^2+q^2+9z^2+pq-3qr+3rp) \hspace{5mm} \cdots \mbox{(答)}
\end{eqnarray}
（２）
\[ x^2+y^2+z^2-xy-yz-zx=\frac{1}{2}(x-y)^2+\frac{1}{2}(y-z)^2+\frac{1}{2}(z-x)^2 \]
と変形できるが, $ p, \ q, \ r $ が正のとき
\[ x-y =p-(-q) >0 \]
なので
\[ x^2+y^2+z^2-xy-yz-zx>0 \mbox{すなわち} p^2+q^2+9z^2+pq-3qr+3rp>0 \]
よって, $f(p, \ q, \ r) =0 $ のとき
\[ p-q-3r=0 \hspace{5mm} \cdots \mbox{①} \]
これより $ 3r= p-q $ を
\[ p^2- 10q – 30r = 11 \hspace{5mm} \cdots \mbox{②} \]
に代入すると
\begin{eqnarray}
p^2- 10q – 10(p-q)=11 \\
p^2-10p-11=0 \\
(p-11)(p+1)=0 \\
\therefore p=11 \hspace{5mm} (\because p>0)
\end{eqnarray}
このとき, ①, ②ともに
\[ q+3r=11 \]
となるが, $q, \ r $ はともに正の整数なので
\[ (q, \ r)=(2, \ 3), \ (5, \ 2), \ (8, \ 1) \]
以上より
\[ (p, \ q, \ r)=(11, \ 2, \ 3), \ (11, \ 5, \ 2), \ (11, \ 8, \ 1) \ \cdots \mbox{(答)} \]
証明
いろいろな証明方法がありますが、まずもっとも一般的な（？）方法でやってみましょう。
$x^3+y^3$に着目すると
対称式の変形
\[ x^3+y^3=(x+y)^3-3xy(x+y) \]
を利用して, $ x+y =A$ と置き換えると
\begin{eqnarray}
x^3+y^3+z^3-3xyz &=& A^3-3xyA+z^3-3xyz \\
&=& A^3+z^3-3xy(A+z) \\
&=& (A+z)(A^2-Az+z^2)-3xy(A+z) \\
&=& (A+z)\left\{ A^2-Az+z^2-3xy \right\} \\
&=& (x+y+z)\left\{ (x+y)^2-(x+y)z+z^2-3xy \right\} \\
&=& (x+y+z)(x^2+y^2+z^2-xy-yx-zx)
\end{eqnarray}
1文字に着目して $x$の3次式とみると
\[ x^3+y^3+z^3-3xyz \]
において $ y, \ z $ を定数とみなして, $x$の3次式と見ると,
\[ \color{red}{x^3} +\color{red}{0x^2}-\color{red}{3yzx}+y^3+z^3 \]
となります。
因数分解後に $x$の1次式 $ x+y+z $ が現れるので, 割り算を実行すると $x$の2次式が商に出てくるはず。
組み立て除法で割り算を実行すると
\begin{array}{ccc}
\underline{-y-z \ } | & 1 & 0 & -3yz & y^3+z^3 \\
& & -y-z & y^2+2yz+z^2 & -(y^3+z^3) \\
\hline
& 1 & -y-z & y^2-yz+z^2 & | \hspace{5mm} 0 \\
\end{array}
となるので
\begin{eqnarray}
x^3+y^3+z^3-3xyz &=& (x+y+z)\left\{ x^2+(-y-z)x+ y^2-yz+z^2 \right\} \\
&=& (x+y+z)(x^2+y^2+z^2-xy-yx-zx)
\end{eqnarray}
縦書きで割り算を実行すると
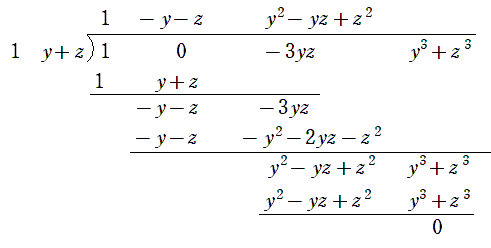
となるので, まったく同じようにして因数分解された積の形に表すことができます。
$x, y, z$ を解に持つ3次方程式を考えると
$x, \ y, \ z$ の3文字の対称性に着目して3次方程式をつくると, カッコイイ証明ができます。
$x, \ y, \ z$ を解に持つ $t$ についての3次方程式は
\[ (t-x)(t-y)(t-z)=0 \]
すなわち
\[ t^3-(x+y+z)t^2+(xy+yz+zx)t-xyz=0 \]
であるが, この3次方程式は $x$を解に持つので
\[ \color{red}{x^3-(x+y+z)x^2+(xy+yz+zx)x-xyz=0} \hspace{5mm} \cdots \mbox{③} \]
が成り立ち, 同様に $y$ と $z$ も解に持つので
\begin{eqnarray}
y^3-(x+y+z)y^2+(xy+yz+zx)y-xyz=0 \hspace{5mm} \cdots \mbox{④} \\
z^3-(x+y+z)z^2+(xy+yz+zx)z-xyz=0 \hspace{5mm} \cdots \mbox{⑤}
\end{eqnarray}
③＋④＋⑤をつくると
\[ x^3+y^3+z^3-(x+y+z)(x^2+y^2+z^2)+(xy+yz+zx)(x+y+z)-3xyz=0 \]
すなわち
\[ x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx) \]
を得る。
$(x+y+z)^3$ を計算すると
これは計算がたいへんで非推奨ですが、3文字を対等に扱うのは、対称式をあつかう基本的な考えかたです。
項数が$3^3$あるので, 展開時にわすれものや重複がないか確認しましょう。
\begin{eqnarray}
(x+y+z)^3 &=& (x+y+z)(x+y+z)(x+y+z) \\
&=& x^3+y^3+z^3 +3x^2y+3y^2z+3z^2x+3xy^2+3yz^2+3zx^2+6xyz
\end{eqnarray}
なので, $x^3+y^3+z^3-3xyz $ をつくって, $xy$などを共通因数としてくくってみると
\begin{eqnarray}
x^3+y^3+z^3-3xyz &=& (x+y+z)^3-3\color{red}{x^2y}-3y^2z-3z^2x-\color{red}{3xy^2}-3yz^2-3zx^2-\color{red}{9xyz} \\
&=& (x+y+z)^3-3\color{red}{xy}(x+y+z)-3\color{blue}{y^2z}-3z^2x-3\color{blue}{yz^2}-3zx^2-6xyz \\
&=& (x+y+z)^3-3xy(x+y+z)-3\color{blue}{yz}(x+y+z)-3zx(x+y+z) \\
&=& (x+y+z) \left\{ (x+y+z)^2-3(xy+yz+zx) \right\} \\
&=& (x+y+z)(x^2+y^2+z^2-xy-yz-zx)
\end{eqnarray}
相加相乗平均へ
\[ \color{blue}{x^2+y^2+z^2-xy-yz-zx=\frac{1}{2}(x-y)^2+\frac{1}{2}(y-z)^2+\frac{1}{2}(z-x)^2} \]
と変形できなくても, 1文字に着目して $x$ の2次式と見ると
\begin{eqnarray}
x^2+y^2+z^2-xy-yz-zx &=& x^2-(y+z)x+y^2+yz+z^2 \\
&=& \left( x-\frac{y+z}{2} \right) ^2- \frac{(y+z)^2}{4} +y^2-yz+z^2 \\
&=& \left( x-\frac{y+z}{2} \right) ^2- \frac{y^2+2yz+z^2}{4} +\frac{4y^2-4yz+4z^2}{4} \\
&=& \left( x-\frac{y+z}{2} \right) ^2 +\frac{3(y-z)^2}{4}
\end{eqnarray}
となるので
\[ x=y \ \mbox{かつ} y=z \ \mbox{かつ} z=x \]
あるいは
\[ x=\frac{y+z}{2} \ \mbox{かつ} y=z \]
すなわち, どちらからも
\[ x=y=z \]
のとき最小値 $ 0 $ を取ることがわかります。これより $x\geqq0, \ y\geqq0, \ z\geqq0$ のとき
\[ x^3+y^3+z^3-3xyz \geqq 0 \]
$ x=\sqrt[3]{a}, \ y=\sqrt[3]{b}, \ z=\sqrt[3]{c} $ とおくと
\[ a+b+c \geqq 3\sqrt[3]{abc} \]
という相加相乗平均の公式も得られます。
【数学のコツ壺】相加相乗平均、使えるかどうかは「積が一定」になるかどうか
実際に相加相乗平均が使えるかどうかは、2文字のときと同じで「積が一定」になるかどうかです。
2文字の場合から、例題で確認してみましょう。
【例題１】$ x>0 $ のとき, $x+\displaystyle \frac{2}{x} $ の最小値を求めよ。
【方針】積を考えると $ x \cdot \displaystyle \frac{2}{x} =$ 一定になるので使えそう。
【解答】$ x>0 $ のとき
\[ x+\displaystyle \frac{2}{x} \geqq 2 \displaystyle \sqrt{x \cdot \frac{2}{x}} = 2 \sqrt{2} \]
となる。等号は
\[ x=\displaystyle \frac{2}{x} \ \mbox{すなわち} \ x=\sqrt{2} \]
のとき成立するので
\[ x=\sqrt{2} \ \mbox{のとき最小値} 2 \sqrt{2} \]
をとる。
【例題２】$ x>0 $ のとき, $x^2+\displaystyle \frac{2}{x} $ の最小値を求めよ。
【方針】積を考えても $ x^2 \cdot \displaystyle \frac{2}{x} $ では一定になりませんが・・・
【解答】$ x>0 $ のとき
\[ x^2+\displaystyle \frac{2}{x} \geqq 3 \displaystyle \sqrt[3]{x^2 \cdot \frac{1}{x} \cdot \frac{1}{x} } = 3 \]
となる。等号は
\[ x^2=\displaystyle \frac{1}{x}=\displaystyle \frac{1}{x} \ \mbox{すなわち} \ x=1 \]
のとき成立するので
\[ x=1 \ \mbox{のとき最小値} 3 \]
をとる。
まとめ
3文字3次の因数分解
\[ x^3+y^3+z^3-3xyz =(x+y+z)(x^2+y^2+z^2-xy-yz-zx) \]
は2文字の対称式と置き換えを使う一般的な方法のほかに、1文字に着目して割り算を実行する方法や、
３文字の対称性をそのままにしても証明することができます。
さらに
\[ x^2+y^2+z^2-xy-yz-zx=\frac{1}{2}\left\{ (x-y)^2+(y-z)^2+(z-x)^2 \right\} \]
と変形するとゼロ以上になることがわかるので, 3文字の相加相乗平均の公式を導けます。
相加相乗平均は「積が一定」なら最小値、「和が一定」なら最大値を求められます。
コメント