二元一次不定方程式の整数解を求めたときに、模範解答と一致しなかったり、空欄をうまく埋めることができないと困ったり悩んだりしたことはありませんか?
不定方程式はその名の如く、解が一つには定まらない方程式なので、答えの表しかたもいくらでもあります。
このブログでは、模範解答と違っていても正しい答えなのかどうか確認したり、テスト中に空欄にうまく埋まらないときでもすぐに埋め直せるようになるためのベクトルを使った簡単な方法をご紹介しています。 一次の不定方程式に自信がないかたは、ぜひ使えるかどうか試してみてください。
5x+7y=12 の整数解を求めてみよう
たとえば $ 5x+7y=12 $ の整数解を求めてみましょう。
$x, \ y $ の係数の小さいほうである $5$に着目して(要は、$5$で割ったときに割り切れない部分に着目して)合同式を立てると、$7=5\times 1+\color{red}{2} $ でも $7=5 \times 2\color{red}{-3} $ でもあるので
\[ \color{red}{2}y \equiv 2 \pmod 5 \]
あるいは
\[ \color{red}{-3}y \equiv 2 \pmod 5 \]
と変形できます。辺々加えて
\[ -y\equiv 4 \pmod 5 \]
両辺$-1$倍すると
\[ y\equiv -4 \pmod 5 \hspace{5mm} \cdots \mbox{①} \]
となりますが、$ -4=5 \times (-1) +1 $ より $-4 \equiv 1 \pmod 5 $ ($-4$も$1$も$5$で割ったときのあまりは同じ)なので
\[ y\equiv 1 \pmod 5 \hspace{5mm} \cdots (k\mbox{は整数 ②}) \]
と表せます。ここから $y$ は $5$で割ると $ 1 $ あまることがわかるので
\[ y=5k+1 \hspace{5mm} \cdots \mbox{②’} \]
と表すことができます。これを与式に代入すると
\begin{eqnarray}5x+7(5k+1)&=& 12 \\
5x+7 \times 5k &=& 5 \\
\therefore x=-7k+1
\end{eqnarray}
以上より、$k$を整数として、整数解は
\[ (x, \ y)=(-7k+1, \ 5k+1) \hspace{5mm} \cdots \mbox{③} \]
と表せる。
y≡-4 のままで計算すると…
上の解答では合同式を ② に変形しましたが、①のまま計算するとどうなるでしょうか?
\[ y\equiv -4 \pmod 5 \hspace{5mm} \cdots \mbox{①} \]
より
\[ y=5k-4 \hspace{5mm} \cdots \mbox{①’} \]
と表すことができます。これを与式に代入すると
\begin{eqnarray}5x+7(5k-4)&=& 12 \\
5x+7 \times 5k &=& 40 \\
\therefore x=-7k+8
\end{eqnarray}
以上より、$k$を整数として、整数解は
\[ (x, \ y)=(-7k+8, \ 5k-4) \hspace{5mm} \cdots \mbox{④} \]
と表せる。
③でも④でもどちらでも構わないのですが、気になってしっくりこないという人は次の方法を試してみてください。
答えから直線を描いてみる
そもそも $ 5x+7y=12 $ は直線の方程式ですが、自分で出した答えや模範解答に乗っている答えから実際に直線を描いてみましょう。もし間違った答えから直線を描くと、模範解答から描ける直線と別のものになってしまいます。
せっかくの機会でもあるので、ベクトルを意識して直線を描いてみましょう。
\[ (x, \ y)=(-7k+1, \ 5k+1) \hspace{5mm} \cdots \mbox{③} \]
を、$k$ でまとめて書き直すと
\[ \left(
\begin{array}{c}
x \\
y
\end{array}
\right) = k \left(
\begin{array}{c}
-7 \\
5
\end{array}
\right) + \left(
\begin{array}{c}
1 \\
1
\end{array}
\right)
\]
となるが、これは $(x, \ y)$ が点 $(1,\ 1)$ を通り方向ベクトルが $(-7, \ 5)$ の直線上にあることを表していて、$k=-1$ のとき点 $(8,\ 4)$ も通ることがわかる。
したがって、③も④も同じ直線上にある、$x, \ y$座標ともに整数値を取る点(格子点という)を表していることがわかります。

練習問題 3x+8y=20 の一般解は?
共通テストの平成30年度試行問題 の一部を使って練習してみましょう。
問題
【問題】空欄に適する数値を求めよ。ただし、空欄クには$4$が入ることが確定しています。
方程式 $3x+8y=20 $ のすべての整数解は, 整数 $n$ を用いて
\[ x= \bbox[2px, border: 3px solid black]{ケコ}+\bbox[2px, border: 3px solid black]{サ}n, \ y=\boxed{ク}-\bbox[2px, border: 3px solid black]{シ}k\]
と表すことができる。
解答・解説
空欄クが$4$なので, 与式に代入すると
\[ 3x+8 \times 4=20 \]
から, 特殊解 $(-4, \ 4)$ が見つかり, $(x, \ y)$ は点 $(-4, \ 4)$ を通る直線上にあることがわかりますが, 無視して合同式で解く練習をしてみましょう。
mod 3 で合同式を立てると$y$の係数が $-1$ になるので連立せずに $y$が求まります。
\[ 3x+8y=20 \hspace{5mm} \cdots \mbox{⑤} \]
より
\[ -y \equiv -1 \pmod 3\]
すなわち
\[ y \equiv 1 \pmod 3\]
を得るので($n$でも良いですが、ぴったり一致しないようなので別の文字を使って)、
\[ y=3k+1 \hspace{5mm} (k\mbox{は定数})\]
と表せる。⑤に代入すると
\begin{eqnarray} 3x+8(3k+1)=20 \\
3x+8 \times 3k =12 \\
x=-8k+4
\end{eqnarray}
これより
\[ \left(
\begin{array}{c}
x \\
y
\end{array}
\right) = k \left(
\begin{array}{c}
-8 \\
3
\end{array}
\right) + \left(
\begin{array}{c}
4 \\
1
\end{array}
\right)
\]
ここで, 空欄クが $4$ になるのは $k=1$ のときなので, 点 $(4, \ 1)$ のほかに点 $(-4 ,\ 4)$ も通る下図のような直線が描ける。
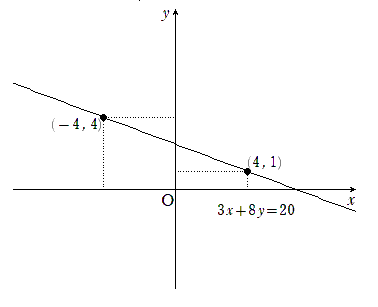
方向ベクトルの向きを逆にして, 点 $(-4 ,\ 4)$ を通る直線を考えて
\[ \left(
\begin{array}{c}
x \\
y
\end{array}
\right) = n \left(
\begin{array}{c}
8 \\
-3
\end{array}
\right) + \left(
\begin{array}{c}
-4 \\
4
\end{array}
\right) \]
すなわち
\[ x=\boxed{-4}+\boxed{8}n, \ y=\boxed{4}-\boxed{3}n \]
を得る。
YouTube動画解説
動画による解説をYouTubeで配信していますので、ぜひそちらもご覧ください。ただし、練習問題の解説はありません。
関連記事
合同式を2本立てて加減法を使って連立して不定方程式を解くやりかたがまだピンとこないけど気になるというかたは、以下のページでより詳しく解説していますのでぜひご活用ください。

コメント