【問題】1次不定方程式 $17x+51y=2023$ を満たす自然数 $x, \hspace{1mm} y$ の組はいくつあるか求めよ。また, このとき, $ \displaystyle \frac{y}{x-3} $ の最大値と最小値を求めよ。
YouTube 動画解説
YouTube でも解説しています。動画のほうがわかりやすいと思うかたはぜひご視聴ください。
考えかた
mod 17 の合同式を考えると, 51も17で割り切れてしまうので
\[ 0 \equiv 2023 \hspace{5mm} \pmod{17} \] となり一瞬ビビります。 要は, 2023も17で割り切れてしまうということですね。実際に割り算を実行していくと \[ 2023=7 \times 17^2 \] ということがわかります。これに気づいたときはビックリしました(笑)。
与式が簡単になったらなったで, 合同式を使うまでもなく一般解が求まるので, 逆に面食らうかもしれないです。
後半の最大・最小は「差の商」の形に着目して, 2点が通る直線の傾きを考えます。より基本的な考えに立ち返って、変数を減らすことでも解決します。
解答
与式は \[ x+3y=119\] と変形できるので, この不定方程式の一般解は \[ (x,y)=(119-3k,k) \hspace{5mm} (kは整数)\] と表せる。
ここで $x,y$ は自然数なので \[ 119-3k <0 \hspace{3mm} \mbox{かつ} \hspace{3mm} k<0 \] すなわち
\[ 0<k< \frac{119}{3} \]
以上より, 自然数解は $k=1, 2, \cdots , 39 $ のときの
\[ 39(\mbox{個}) \hspace{5mm} \cdots (\mbox{答})\]
ある。
次に $ \displaystyle \frac{y}{x-3} $ は 2点$(3,0), (x,y) $を通る直線の傾きと一致するので, 直線$x+3y=119$上の39個の点と $(3,0)$ が作る直線の傾きを考えて \begin{eqnarray} (x,y)=(5,38) \mbox{のとき, 最大値} \frac{38}{5-3}=19 \cdots (\mbox{答}) \\ (x,y)=(2,39) \mbox{のとき, 最小値} \frac{39}{2-3}=-39 \cdots (\mbox{答}) \end{eqnarray}
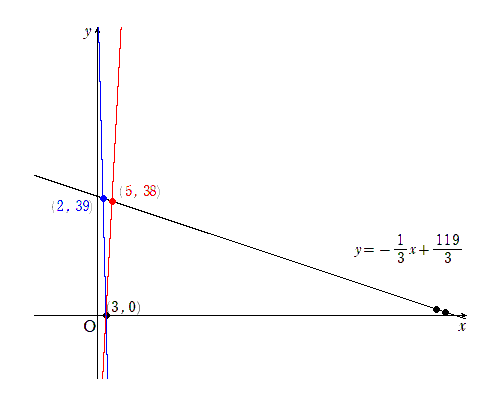
【別解】x, y を k で表すと
一般解を代入すると \begin{eqnarray} \frac{y}{x-3} &=&\frac{k}{119-3k-3}\\ &=& \frac{k}{116-3k} \end{eqnarray} となるので, 分子は増加, 分母は減少する。ただし, 分母は $1 \leqq k \leqq 38 $ のときは正だが $ k=39 $のときのみ負となることに注意すると \begin{eqnarray} k=38 \mbox{すなわち} \hspace{3mm} (x,y)=(5,38) \mbox{のとき, 最大値} \frac{38}{116-3 \times 38}=19 \cdots (\mbox{答}) \\ k=39 \mbox{すなわち} \hspace{3mm} (x,y)=(2,39) \mbox{のとき, 最小値} \frac{39}{116-3 \times 39}=-39 \cdots (\mbox{答}) \end{eqnarray} となる。


コメント