【問題】空欄に適した数または式を入れよ。
$2016$ と $2800$ の最大公約数は $d= \boxed{\color{black}{\text{(ア)}}} $ であり, 最小公倍数は $\boxed{\color{black}{\text{(イ)}}}$ である。 また, 方程式 $2016x+2800y=d$ の整数解のうち, $ |x|+|y|$ が最小になるのものは $x=\boxed{\color{black}{\text{(ウ)}}}$ , $y=\boxed{\color{black}{\text{(エ)}}}$ である。
【前半方針】最大公約数は素因数分解。できなければ、ユークリッドの互除法
前半部分の最大公約数・最小公倍数は、素因数分解が速そうです。約数がパッと見つからない場合に備えて、ユークリッドの互除法を練習しておきましょう。
2数 $A, B$ の最大公約数を$G$, 最小公倍数を$L$ としたときに $ AB=GL $ の関係があることも, 使ってみます。
【前半(最大公約数・最小公倍数問題)解答・解説】
【方針1】素因数分解もどきの利用
限られた時間のなかで効率よく解くには、素因数に完全に分解しないほうがおそらく簡単です。
【解答】
\begin{eqnarray}2800&=&100\cdot 28= 25 \cdot 4 \cdot 4 \cdot 7 \hspace{2mm}(=A\mbox{とおく})\\ 2016&=&4\cdot 4\cdot7 \cdot 18\hspace{2mm}(=B\mbox{とおく}) \end{eqnarray}
なので
$$ d=4 \cdot 4 \cdot 7 = 112 \hspace{5mm} \cdots \mbox{(ア)の(答)} $$
ここで, 最小公倍数を$l$とすると, $AB=dl$なので
\begin{eqnarray}(25 \cdot 4 \cdot 4 \cdot 7) \cdot (4\cdot 4\cdot7 \cdot 18)=4 \cdot 4 \cdot 7 \cdot l \\ \mbox{∴}\hspace{2mm} l=2800 \cdot 18 =50400 \hspace{5mm} \cdots \mbox{(イ)の(答)}\end{eqnarray}
【方針2】ユークリッドの互除法を利用して, どんどん余りで割って行く
まず大きい数字を小さい数字で割ります。
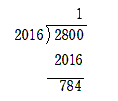
続いて, 小さい数字を余りで割ります。どんどん繰り返し余りが0になるまで続けます。
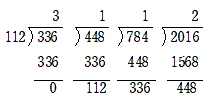
イメージとしては, 縦横それぞれ2016と2800の長方形を, できるだけ大きな正方形で切り取っていく感じになります。
余りが生じる間は, その余りに相当する一辺の長さの正方形(Gとする)で切り取っていき, 最終的にはこの正方形Gで初めの長方形を隙間なく敷き詰めることができます。
ここでは, 2016と2800を縦横とする長方形を, 一辺の長さ112の正方形で敷き詰めることができるので, この数が最大公約数となります。
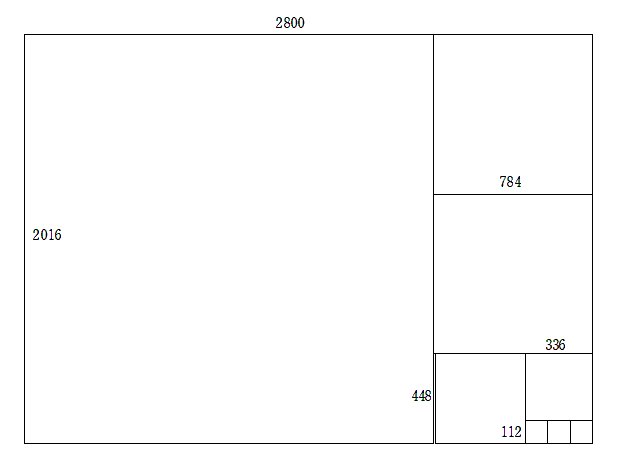
【解答】
ユークリッドの互除法より
\begin{eqnarray} 2800 &=& 2016 \times 1 + 784 \\ 2016 &=& 784 \times 2 + 448\\ 784 &=&448 \times 1 + 336 \\ 448 &=& 336 \times 1 +112 \\ 336 &=& 112 \times 3 +0 \end{eqnarray}
以上より
$$ d=112\hspace{5mm} \cdots \mbox{(ア)の(答)} $$
(最小公倍数については, 【方針1】と同様)
【後半(一次不定方程式問題)解答・解説】
与式の両辺を最大公約数$d$で割ることで, より簡単な形にできます。
そのあとのやりかたはいろいろありますが, 係数の小さなほうを法に合同式を作ってみます。合同式は割り算以外は, 普通に計算できます。
【解答】
$ 2016x+2800y=112 $ より$$ 18x+25y=1 \hspace{5mm} \cdots \mbox{①}$$
ここで, $ 25=18 \times 1 +7 $ , あるいは $ 25=18 \times 2 -11 $ なので, ①式は
\begin{eqnarray} \begin{cases} 7y &\equiv& 1 \hspace{5mm} \hspace{5mm} \cdots \mbox{②} \\ -11y &\equiv& 1 \hspace{5mm} \hspace{5mm} \cdots \mbox{③} \end{cases} (\mbox{mod} \hspace{2mm} 18) \end{eqnarray}
の2通りに変形でき, ② $ \times 3 + $ ③ $ \times 2 $ を作ると
\begin{eqnarray} 21y-22y & \equiv & 5 \\ -y & \equiv & 5 \\ \mbox{∴}\hspace{2mm} y & \equiv & -5\hspace{2mm} (\mbox{mod} \hspace{2mm} 18) \end{eqnarray}
よって
$$ y=18k-5 \hspace{2mm} ( k \mbox{は整数})$$
①に代入すると
\begin{eqnarray} 18x+25(18k-5)=1 \\ 18x+25 \cdot 18k= 126 \\ x =-25k+7 \end{eqnarray}
これらより
\begin{eqnarray} | x | + | y | &=& |-25k+7 | + |18k-5 | \\ &=& \begin{cases} -43k+12 \hspace{5mm}(k \mbox{≦} 0 \mbox{のとき} )\\ 43k-12\hspace{5mm}(1 \mbox{≦} k \mbox{のとき} ) \end{cases}\end{eqnarray}
なので, $k=0$のときと$k=1$のときの$|x|+|y|$の値を比較して, $k=0$, すなわち
$$ x=7, y=-5 \hspace{5mm}\cdots \mbox{(ウ,エ)の(答)}$$
のときに, $|x|+|y|$は最小となることがわかる。

コメント