$4$次関数 $y=f(x) $ のグラフで表される曲線 $C$ と直線 $l$ について, 次のような条件Aを考える。
条件A: 曲線 $C$ と直線 $l$ が $x = x_1, x_2, x_3, x_4 (x_1 < x_2 < x_3 < x_4) $ で交点を持ち,曲線 $C$ と直線 $l$ で囲まれた図形の$3$つの部分の面積について,$ S_1 = S_3 $ と $ S_1 + S_3 = S_2 $ が成り立つ。ここで,$S_1, S_2, S_3 $ はそれぞれ $x_1 \leqq x\leqq x_2, \ x_2 \leqq x \leqq x_3, \ x_3 \leqq x \leqq x_4$ を満たす部分の面積を表す。
(a) 曲線 $ y = g(x) = x^4 – \displaystyle \frac{18}{5}x^2+a $ と直線 $y=0$ が条件A を満たすとする。このとき,$x_3= b, \ x_4 = c$ とおくと, \[ \int ^c_0 g(x)dx =\displaystyle \frac{ \boxed{\mbox{ア}}}{\boxed{\mbox{イ}}}c^5 – \displaystyle \frac{ \boxed{\mbox{ウ}}}{\boxed{\mbox{エ}}}c^3 +ac=\boxed{\mbox{オ}} \] となり,\[ a=\displaystyle \frac{ \boxed{\mbox{カ}}}{\boxed{\mbox{キ}}}, \ b= \displaystyle \frac{\sqrt{\boxed{\mbox{クケ}}}}{ \boxed{\mbox{コ}}}, \ c=\displaystyle \sqrt{\boxed{\mbox{サ}}} \] となる。
(b) 曲線 $ y = h(x) = x^4 + 4x^3 +\displaystyle \frac{12}{5}x^2 −\displaystyle \frac{6}{5}x + \displaystyle \frac{12}{5} $ に対して条件A を満たす直線の方程式を求めよう。まず,\[ h(x) = (x + d)^4 − \frac{\boxed{\mbox{シス}}}{\boxed{\mbox{セ}}}(x + d)^2 + \boxed{\mbox{ソ}} (x + d) + \boxed{\mbox{タ}} \] と変形する。ただし,$ d = \boxed{\mbox{チ}} $ である。
ここで,$ h_1(x) = (x + d)^4 −\displaystyle \frac{\boxed{\mbox{シス}}}{\boxed{\mbox{セ}}}(x + d)^2 $ とおくと,曲線 $ y = h_1(x) $ に対して条件A を満たす直線の方程式は \[ y = \frac{\boxed{\mbox{ツテ}}}{\boxed{\mbox{ト}}} \] である。したがって,求める直線の方程式は \[ y = \boxed{\mbox{ナ}} x +\frac{\boxed{\mbox{ニヌ}}}{\boxed{\mbox{ネ}}} \] である。
(c) 曲線 $ y = x^4 − 3x^2 + 2x + 2 $ に対して条件A を満たす直線の方程式は \[ y = \boxed{\mbox{ノ}} x + \frac{\boxed{\mbox{ハ}}}{\boxed{\mbox{ヒ}}} \] である。
数学のコツ壺
対称性に着目
「偶関数は $y$軸に関して線対称、奇関数は原点に関して点対称」です。
$ y = g(x) = x^4 – \displaystyle \frac{18}{5}x^2+a $ が偶関数であることに気づけるかが, まず大切です。
引き算は後ろが基準
$ y= h(x) = (x + d)^4 − \frac{\boxed{\mbox{シス}}}{\boxed{\mbox{セ}}}(x + d)^2 + \boxed{\mbox{ソ}} (x + d) + \boxed{\mbox{タ}} $ は
\[ y=x^4-\frac{\boxed{\mbox{シス}}}{\boxed{\mbox{セ}}}x^2+\boxed{\mbox{ソ}} x + \boxed{\mbox{タ}}\]
を $x$ 軸方向にどう平行移動したものかすぐわかりますか?
$x$軸方向に $-d$だけ平行移動したものになるのですが, わかりにくい場合は簡単な例で実験しましょう。
$y=x^2$ と $y=(x-2)^2 $ で考えると \[ y=(x-2)^2 \mbox{は} y=x^2 \mbox{を} x\mbox{軸方向に}2\mbox{だけ平行移動したもの} \]
です。
公式としては $y=f(x)$ を $x$軸方向に $\alpha $, $y$軸方向に $\beta$ 平行移動すると \[ y- \beta = f(x-\alpha ) \] となりますが, これは感覚的には \[ \mbox{点}(\alpha, \ \beta) \mbox{を基準にして} y=f(x) \mbox{を描く(見る)と} y- \beta = f(x-\alpha ) \mbox{になる} \] ということです。
面積を考えるときも, 引き算の後ろが基準
(1) では$ y = g(x) = x^4 – \displaystyle \frac{18}{5}x^2+\frac{9}{5} $ と直線 $y=0$ が条件Aを満たしますが, 直線から4次関数をみたとき, すなわち引き算をつくったときにその結果が $ x^4 – \displaystyle \frac{18}{5}x^2+\frac{9}{5} $ になれば, どんな場合も条件Aを満たします。
【関連記事】【基礎】2次関数と接線がつくる面積
解答
ア 1, イ 5, ウ 6, エ 5, オ 0,
カ 9, キ 5, クケ 15, コ 5, サ 3,
シス 18, セ 5, ソ 2, タ 3, チ 1
ツテ -9, ト 5, ナ 2, ニヌ 16, ネ 5
ノ 2, ハ 3, ヒ4
解説
(a) \[ y = g(x) = x^4 – \displaystyle \frac{18}{5}x^2+a \hspace{5mm} \cdots \mbox{①} \] は偶関数で $y$軸に関して対称なので
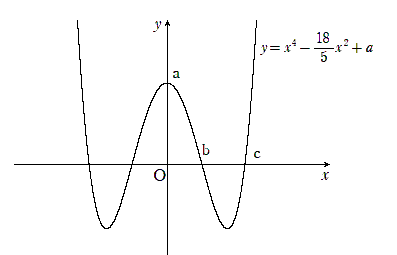
$ x_3=b, \ x_4=c $ ならば \[ x_1=-c, \ x_2=-b \] となるので
\begin{eqnarray}
g(x) &=& (x+c)(x+b)(x-b)(x-c) \\
&=& (x^2-b^2)(x^2-c^2) \\
&=& x^4-(b^2+c^2)x^2+b^2c^2
\end{eqnarray}
と変形できるが, これは①と一致するので
\begin{eqnarray}
b^2+c^2= \frac{18}{5} \hspace{5mm} \cdots \mbox{②}\\
b^2c^2=a \hspace{5mm} \cdots \mbox{③}
\end{eqnarray}
また, $ \displaystyle \frac{S_2}{2}=S_3$ より \begin{eqnarray} \int ^c_0 g(x)dx &=& \int ^c_0 (x^4 – \displaystyle \frac{18}{5}x^2+a ) dx \\
&=& \left[ \frac{1}{5}x^5 – \displaystyle \frac{6}{5}x^3+ax \right] ^c_0 \\
&=& \frac{\boxed{1}}{\boxed{5}}c^5 – \displaystyle \frac{\boxed{6}}{\boxed{5}}c^3+ac \\
&=& \boxed{0} \\
\therefore c^4-6c^2+5a =0 \ (\because c>0)
\end{eqnarray}
さらに③より $ a=b^2c^2 $ を代入して
\begin{eqnarray}
c^4-6c^2+5b^2c^2 =0 \\
\therefore c^2+5b^2 =6 \ (\because c>0) \hspace{5mm} \cdots \mbox{④}
\end{eqnarray}
④ $-$ ② より
\begin{eqnarray}
4b^2=\frac{12}{5} \\
\therefore b^2=\frac{3}{5}
\end{eqnarray}
② とから \[ c^2=3 \]
③ に代入して \[ a=\frac{3}{5} \cdot 3=\frac{\boxed{9}}{\boxed{5}}\]
$ b>0, c>0 $ より \[ b=\frac{ \sqrt{\boxed{15}}}{\boxed{5}}, \ c=\sqrt{\boxed{3}} \]
(b)
$ h(x) $ の $x^3$の係数$4$ は $(x+d)^4$ を展開することで得られるが \[ (x+d)^4=x^4+ {}_4 \mathrm{C}_1 dx^3+ \cdots \]
とから \[ d=1 \] ここで
\[ h(x) = (x + 1)^4 − p(x + 1)^2 + q (x + 1) + r \]
とおくと
\begin{eqnarray}
h(x) &=& x^4+4x^3+6x^2+4x+1 -p(x^2+2x+1)+qx+q +r \\
&=& x^4 +4x^3 +(6-p)x^2+(4-2p+q)x+1-p+q+r \end{eqnarray}
これは $ h(x) = x^4 + 4x^3 +\displaystyle \frac{12}{5}x^2 −\displaystyle \frac{6}{5}x + \displaystyle \frac{12}{5} $ と一致するので
\begin{eqnarray}
6-p=\frac{12}{5} \\
4-2p+q = -\frac{6}{5} \\
1-p+q+r= \frac{12}{5} \end{eqnarray}
これらを解いて \[ p=\frac{\boxed{18}}{\boxed{5}}, \ q=\boxed{2}, \ r=\boxed{3} \] このとき \[ h(x) = (x + 1)^4 − \frac{18}{5}(x + 1)^2 + 2 (x + 1) +3 \] (1) の結果より \[ y= g(x) = x^4 – \displaystyle \frac{18}{5}x^2+\frac{9}{5} \] と $y=0$ は条件A を満たすので, $ y=g(x) $ を $x$軸方向に$-1$だけ平行移動した \[ y=g(x+1) =(x + 1)^4 − \frac{18}{5}(x + 1)^2+\frac{9}{5} \] と $y=0$ も条件A を満たす。ここで \[y= h_1(x) = (x + 1)^4 −\frac{18}{5}(x + 1)^2 \] とで条件A を満たす直線を $ y=l_1(x) $ とおくと \[ h_1(x)-l_1(x)=g(x+1) -0 \] を満たすので, これより \[ l_1(x)=\frac{\boxed{-9}}{\boxed{5}}\] 同様に \[ y=h(x) \] とで条件A を満たす直線を $ y=l_2(x) $ とおくと \[ h(x)-l_2(x)=g(x+1) -0 \] を満たすので, \[ l_2(x)=\boxed{2}x+\frac{\boxed{16}}{\boxed{5}}\]
(c) 曲線 $ y = x^4 − 3x^2 + a’ \ (a’>0)$ と直線 $y=0$が条件A を満たす場合を考え, $x>0$ での交点を小さいほうから $ b’,\ c’ $ とすると恒等的に \[ (x-b’)(x-c’)(x+b’)(x-c’)=x^4-3x^2+a’ \] が成り立つので\begin{eqnarray}
b’^2+c’^2= 3 \hspace{5mm} \cdots \mbox{②’}\\
b’^2c’^2=a’ \hspace{5mm} \cdots \mbox{③’}
\end{eqnarray}
また, $ \displaystyle \frac{S_2}{2}=S_3$ より \[ \int ^{c’}_0 (x^4 -3x^2+a’ ) dx =0 \] すなわち
\[ \frac{1}{5}c’^5-c’^3+a’c’ =0 \]
を得るが $c’>0$より \[ c’^4-5c’^2+5a’ =0 \]
③’ より $ a’=b’^2c’^2 $ を代入して
\[ c’^4-5c’^2+5b’^2c’^2 =0 \]
$c^2>0 $ より
\[ c’^2+5b’^2 =5 \]
②’, とから \[ b’^2=\frac{1}{2}, c’^2=\frac{5}{2}\]
このとき \[ a’=\frac{5}{4} \]
よって, 求める直線を $y=l_3(x) $ とおくと \[ x^4 − 3x^2 + 2x + 2-l_3(x)=x^4 -3x^2+\frac{5}{4} -0 \] \[
\therefore l_3(x)=\boxed{2}x+\frac{\boxed{3}}{\boxed{4}} \]

コメント