平均変化率
「直線の傾き」に相当するものを、曲線で考えます。
曲線上に2点をとると、その2点をつなぐことにより直線ができます。その直線の傾きが平均変化率です。2点を(x1,y1),(x2,y2)とすると式では
となります。直線の傾きの公式
が浮かんでくればOKです。ただ、曲線上では直線の傾きのように一通りに決まるのではなく2点の選びかたによって変化します。
ピンとこない場合は、実験しましょう!
引き算は後ろが基準なので、(x1,y1)を固定して動かないようにして、(x2,y2)を動かしてみます。
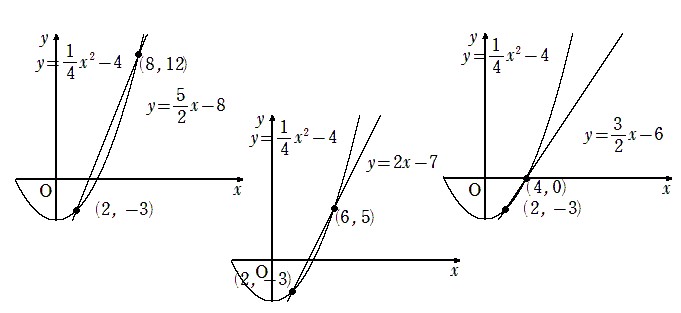
ここでは、放物線 y=1/4x^2-4 とその上に、(x1,y1)=(2,-3)をとり(x2,y2)を放物線上にいくつか選んで、2点を通る直線の傾きを考えてみます。すると下図のようになります。
(x2,y2)の選びかたによって当然直線の傾きは変化しますが、ここであることに気づきませんか?
もうすこし補足すると、(x2,y2)を(x1,y1)に近づけてくると、あることに気づきませんか?
そうです。直線が(x1,y1)における接線に使づいてきます。
ですから、(x2,y2)を限りなく(x1,y1)に近づけると(x1,y1)における接線の傾きが得られます。これを微分係数と定義し
とします。
関数を一般化して f(x)とすると点は(x1,f(x1))などとあらわせるので,x=x1における微分係数f'(x1)は
となります。
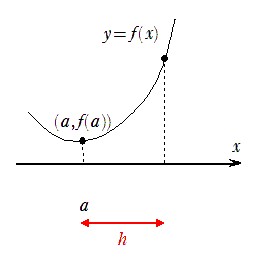
ここまでは、2点を曲線上にとりましたが、1点ともう1点との幅を考えても同じようにできます。
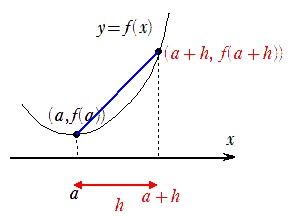
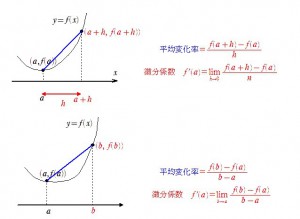
一般的な関数 y=f(x)上で、1点のx座標をaとして幅をhとします。
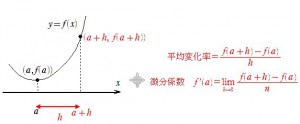
すると、2点は(a,f(a))と(a+h,f(a+h))となるので、平均変化率と微分係数は
となります。
【まとめ】平均変化率を「2点」でも「1点ともう1点との幅」でも、どちらでも考えられるようにしよう
動画をYouTubeにアップしていますので、こちらもご参考に。
コメント