みなさん、こんにちは。
きょうは、2次関数と2本の接線の性質についてです。
次の問題を考えてみてください。制限時間は1分です。
【問題A】曲線$ \mathrm{C} : y=x^2-5x+1 $上の点$\mathrm{A}(4,-3) $ における接線を$m$, 点$\mathrm{B}(0,1)$ における接線を$n$とする。これらの2接線の交点の$x$座標は $ \boxed{\color{black}{\text{ア}}} $である。
また, $l$, $m$と曲線$\mathrm{C}$とで囲まれた部分の面積は$\frac{\boxed{\color{black}{\text{イウ}}}}{\boxed{\color{black}{\phantom{1}\text{エ}\phantom{1}}}}$である。
ポイント
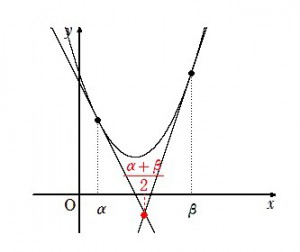
2次関数の2接線の交点のx座標は、2接点のちょうど真ん中にある
解答
2次関数の2接線$m$と$n$の接点の$x$座標はそれぞれ$4, 0$ なので、接線の交点の$x$座標は
\[ \boxed{\color{black}{\text{2}}} \hspace{10mm} \cdots \mbox{アの(答)}
\]
であり, 囲む部分は
のようになるので、求める面積を $\mathrm{S}$ とすると
\begin{eqnarray}
S&=&\int^2_0 x^2 dx + \int^4_2 (x-4)^2 dx \hspace{10mm} \cdots \mbox{(※)} \\
&=& \left[\ \frac{1}{3}x^3 \right]^2_0 + \left[\ \frac{1}{3}(x-4)^3 \right]^4_2 \\
&=& \frac{8}{3} + \frac{8}{3} \\
&=& \frac{\boxed{\color{black}{\text{16}}}}{\boxed{\color{black}{\text{3}}}} \hspace{10mm} \cdots \mbox{イウエの(答)}
\end{eqnarray}
接線の交点を一般的に計算してみると
確認のために, 一般的に2次関数上の2点から接線を引いて, その交点を計算してみましょう。
2次関数 $ y=ax^2+bx+c \hspace{2mm} (a \neq 0) $ 上に, $x$座標が$ \alpha , \beta (\alpha < \beta)$ となる2点を考える。 $ y'=2ax+b $ だから, $x=\alpha$ なる点における接線の方程式は \[ y-(a\alpha ^2+b\alpha +c) =(2a \alpha +b)(x- \alpha) \] すなわち \[ y =(2a \alpha +b)x- a\alpha^2+c \hspace{10mm} \cdots \mbox{①} \] 同様に, $x=\beta$ なる点における接線の方程式は \[ y =(2a \beta +b)x- a\beta^2+c \hspace{10mm} \cdots \mbox{②} \] なので, ①-②を作ると \begin{eqnarray} 2a( \beta -\alpha)x - a( \beta ^2- \alpha ^2) = 0 \\ a( \beta -\alpha)\{2x-(\beta+\alpha)\} = 0 \end{eqnarray} $ a \neq 0, \hspace{2mm} \alpha < \beta $ なので, 2つの接線①, ②の交点の$x$座標は \[ x=\frac{\alpha + \beta}{2} \] となる。
面積は下側の曲線を基準にして上側の曲線を見る
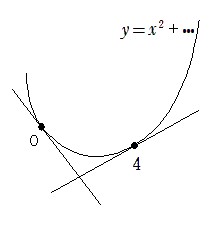
グラフもきれいに描く必要ないですが, せっかくなので接線も含めて描き直してみると
となります。
ここで, 改めて面積計算の(※)式を見ると, 積分の計算は
\[\int^2_0 x^2 dx + \int^4_2 (x-4)^2 dx
\]
$ y=x^2-5x+1 $ も $ y=3x-15 $ も $y=-5x+1$ も使っていません。
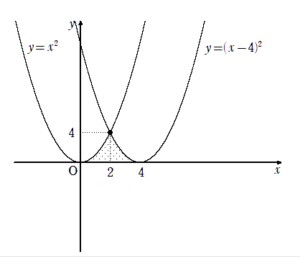
この計算で求めている面積は, 下図の2曲線と $x$軸で囲まれた部分です。
囲まれた部分は, 直線$x=2$に関して対称なので, 面積も半分だけ計算して2倍にするともっと簡単。
要は, 面積計算では, 上側の曲線から下側の曲線を引いたもの, すなわち, 下側の曲線を基準にして上側の曲線をみたらどうなるかだけわかればよいのです。


コメント