3乗根(m+1)-3乗根m<1/48 を満たすmの最小値(東京医科大2020)

YouTube では同じ東京医科大2013年の問題の解説を行う予定です。

教育系YouTuberの鈴木貫太郎さんが紹介していた問題で、私も分子を有理化しました。平均値の定理もありそうかなと思いましたが数Ⅲ嫌いという単純な理由で避けましたが、同じく数Ⅲの面積比較が使える解法があると知ってなるほどなぁと思いこちらでも紹介することにしました。

問題

不等式 $$\sqrt[3]{m+1} \hspace{1mm} – \sqrt[3]{m} < \frac{1}{48}$$ を満たす正の整数 $m$の最小値は$\boxed{\color{black}{\text{(アイ)}}}$である

【数学のコツ壺】f(n+1)-f(n) がどう見える？

$f(n+1)-f(n)$ が見えたら
(1) $f(b)-f(a)$ と見て平均値の定理へ持ち込む
ことが多いかもしれないですが、
(2) $F(n+1)- F(n)$ と見えると $F'(x)=f(x)$として
$$F(n+1)-F(n)=\int^{n+1}_n f(x) dx$$ として面積比較へ持ち込むこともできるかもしれません

解答

$F(x)=x^{\frac{1}{3}} \hspace{3mm}(x>0)$ さらに $f(x)=F'(x)$ とすると

$$\begin{eqnarray} f(x)&=& \frac{1}{3}x^{-\frac{2}{3}} \\ f'(x)&=& \frac{1}{3} \cdot \displaystyle(-\frac{2}{3} ) x^{-\frac{5}{3}} \\ &=& -\frac{2}{9}x^{-\frac{5}{3}} \end{eqnarray}$$

より $x>0$ で $f(x)$は単調減少。

一方で

$$\sqrt[3]{m+1} \hspace{1mm} – \sqrt[3]{m} = \int^{m+1}_m \frac{1}{3}x^{-\frac{2}{3}} dx$$

と変形できるが, $\displaystyle\frac{1}{3}x^{-\frac{2}{3}} = \displaystyle\frac{1}{48}$ を解くと

$$\begin{eqnarray} \frac{1}{3}x^{-\frac{2}{3}} &=& \frac{1}{48} \\ x^{-\frac{2}{3}} &=& \frac{1}{16} \\ \frac{1}{x^{\frac{2}{3}}} &=& \frac{1}{16} \\ x^{\frac{2}{3}} &=& 16 \\ x^{\frac{1}{3}} &=& 4 \\ x &=& 64 \\ \end{eqnarray}$$

なので, 面積比較をすると

$$\cdots > \int ^{63}_{62} \frac{1}{3}x^{-\frac{2}{3}} dx >\int ^{64}_{63} \frac{1}{3}x^{-\frac{2}{3}} dx >1 \cdot \frac{1}{48} > \int ^{65}_{64} \frac{1}{3}x^{-\frac{2}{3}} dx > \int ^{66}_{65} \frac{1}{3}x^{-\frac{2}{3}} dx > \cdots$$

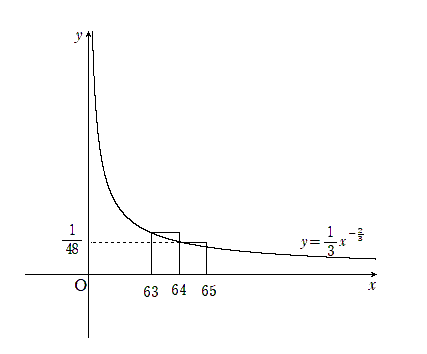
以上より, 求める $m$の最小値は

$$m=64 \hspace{5mm} \cdots (\mbox{答})$$

練習問題

不等式 $$\log {(n+9)} – \log {(n+8)} < \frac{1}{100}$$ を満たす正の整数 $n$の最小値を求めよ。ただし, 対数は自然対数である。

練習問題の解説はYouTubeで行っています。