【問題】赤玉が1個、白玉が2個入っている袋の中から、無作為に1個の球を取り出し、色を確認したら元に戻し、さらに同じ色の球を1個袋の中に入れる。このとき、次の確率を答えよ。
(1) 3回とも赤玉を取り出す確率
(2) 3回目に赤玉を取り出す確率
(3) 3回目に赤玉を取り出したとき、2回目も赤玉を取り出す条件つき確率
答
\[
(1) \frac{1}{10} \hspace{5mm} (2) \frac{1}{3} \hspace{5mm} (3) \frac{1}{2}
\]
ポイント
・サンプルをつくって実験する
・条件付き確率は、基準(分母)が全体から一部に変わる
解答・解説
(1)の実験
袋の中の状態の図を描いてみると
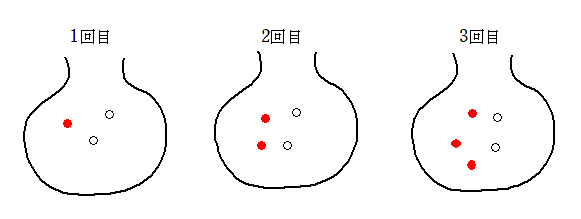
のようになるので、これを元に1回1回の赤玉を取り出す確率を確認できます。
同時に、(2)以降のウォーミングアップにもなります。
(1)の解答
赤玉を取り出すたびに、1個ずつ袋の中の赤玉が増えるので、3回とも赤玉を取り出す確率は
\[
\frac{1}{3} \cdot \frac{2}{4} \cdot \frac{3}{5} = \frac{1}{10} \hspace{20mm} \cdots \mbox{①}
\]
(2)の実験
3回目に赤を取り出すのは、1,2回目に(1)の赤→赤の他に、赤→白、白→赤、白→白の3パターンがある。
これらを(1)と同じように、丁寧に計算する。
(2)の解答
i) 赤、白、赤の順で取り出す確率は
\[
\frac{1}{3} \cdot \frac{2}{4} \cdot \frac{2}{5} = \frac{1}{15}
\]
ii) 白、赤、赤の順で取り出す確率は
\[
\frac{2}{3} \cdot \frac{1}{4} \cdot \frac{2}{5} = \frac{1}{15} \hspace{20mm} \cdots \mbox{②}
\]
iii) 白、白、赤の順で取り出す確率は
\[
\frac{2}{3} \cdot \frac{3}{4} \cdot \frac{1}{5} = \frac{1}{10}
\]
i), ii), iii) および (1)の結果とから、求める確率は
\[
\frac{1}{15} + \frac{1}{15} + \frac{1}{10} + \frac{1}{10} =\frac{2+2+3+3}{30} =\frac{1}{3}
\]
(3)の実験
ベン図などを描くことで、3回目に赤が出る確率を基準にして、2,3回目ともに赤が出る確率を求めればよいことを確認しましょう。
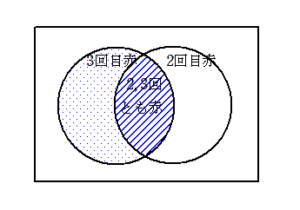
(3)の解答
①,②より、2,3回目にともに赤が出る確率は
\[\frac{1}{10} + \frac{1}{15} = \frac{5}{30} = \frac{1}{6}
\]
なので、3回目に赤玉を取り出したとき、2回目も赤玉を取り出す条件つき確率は
\[
\frac{\frac{1}{6}}{\frac{1}{3}}=\frac{1}{2}
\]

コメント