条件付き確率の問題で、工場から出荷された商品に不良品が混ざっているタイプのものがあります。
今回は、この問題を簡単に解くコツを紹介します。
問題
【問題】ある地域ではA工場とB工場でマスクを製造しているが、不良品が現れる確率はA工場が3%、B工場が7%である。また、A工場とB工場で製造するマスクの割合は5:2である。このとき、次の問いに答えよ。
(1)製品の中から1個を取り出したとき、それが不良品である確率を求めよ。
(2)不良品であったとき、そのマスクがA工場で製造したものである確率を求めよ。
コツ
【コツ】条件付き確率は、分母が変わる(新たな分母は「~のとき」)
【コツ】コロナ問題では、新たな分母を一辺の長さ1の正方形上で確認しよう
YouTube動画解説
同じ問題をYouTubeで解説しています。
条件付き確率そのものがよくわからない苦手な人は、こちらの動画を御覧ください。
(1)解答
(1)A工場で製造するマスクは全体の $ \displaystyle \frac{5}{7} $, B工場で製造するのは $ \displaystyle \frac{2}{7} $ なので, 求める確率は
\[ \frac{5}{7} \times \frac{3}{100} +\frac{2}{7} \times \frac{7}{100}=\frac{29}{700} \hspace{1cm} \cdots \mbox{(答)} \]
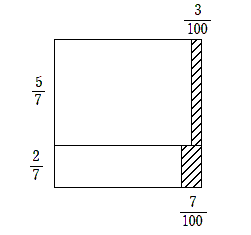
(2)考え方
「不良品であったとき」という問題文から、求めるべき条件付き確率の基準となる分母は、不良品であり確率、すなわち、上図の斜線部。
分子は、斜線部のうちの上側の長方形部分です。
(2)解答
求める確率は
\[ \frac{\frac{5}{7} \times \frac{3}{100}}{ \frac{29}{700}}=\frac{15}{29} \hspace{1cm} \cdots \mbox{(答)} \]
【別解】正方形が考えにくい人は、全マスク数を適当に決めよう
一辺の長さ1の正方形を考えるのが難しいという人は、全体のマスクの数を割合ではなく具体的な数で考えましょう。
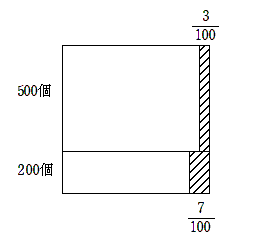
別解
(1)A工場とB工場のマスクの製造割合が5:2なので, A工場で500個, B工場で200個作ったとすると, 不良品の数は
\[ 500 \times \frac{3}{100} + 200 \times \frac{7}{100} = 29 \]
よって, 求める確率は
\[ \frac{29}{500+200}=\frac{29}{700} \hspace{1cm} \cdots \mbox{(答)} \]
(2)(1)より, すべての不良品29個のうち,A工場で製造されたのは15個あるので, 求める確率は
\[ \frac{15}{29}\hspace{1cm} \cdots \mbox{(答)} \]

コメント