条件付き確率の問題で、病原菌に関するものがあります。
今回は、この問題を簡単に解くコツを紹介します。
問.ある地域で病気Xに感染している人の割合が0.01%であるとする。この病気Xの検査では、感染している人は99%の確率で陽性と判定され、感染していない人も1%の確率で陽性と判定されてしまう。このとき、次の問いに答えよ。
(1)この地域に住む人がこの検査を受けて陽性と判定されたとき、この人が本当に病気Xに感染している確率を求めよ。
(2)この人が再検査を受け再び陽性と判定されたとき、この人が本当に病気Xに感染している確率を求めよ。
コツ
【コツ】条件付き確率は、分母が変わる(新たな分母は「~のとき」)
【コツ】コロナ問題では、新たな分母を一辺の長さ1の正方形上で確認しよう
(1)方針
一辺の長さ1の正方形で全体を表し、感染している人と感染していない人に分けます。

続いて、検査を受けて陽性になる人の割合を斜線にします。
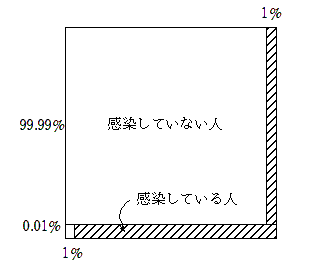
2つの斜線部分(検査で陽性とされる確率)に対する、横長の斜線部分(感染していて、陽性とされる確率)が、求めるべき条件付き確率になります。
(1)解答
検査で陽性となる確率は
\[ \frac{0.01}{100} \times \frac{99}{100} +\frac{99.99}{100} \times \frac{1}{100}=\frac{0.99+99.99}{10000} \]
そのうち、感染していて陽性となっている確率は
\[ \frac{0.01}{100} \times \frac{99}{100} = \frac{0.99}{10000} \]
なので、求める条件付き確率は
\[ \frac{\frac{0.99}{10000}}{\frac{0.99+99.99}{10000}}= \frac{0.99}{0.99+99.99}= \frac{0.01}{0.01+1.01} =\frac{1}{102} \cdots \mbox{(答)} \]
(1)別解・・・【方針】人口を具体的に設定する
全体を1とするのがわかりにくい場合は、検査対象の人数を設定してみましょう。
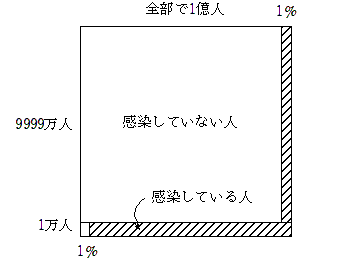
別解解答
ある地域の人口を1億人とする。検査で陽性になる人は
感染している人1万人のうちの $ 10000 \times \frac{99}{100} = 9900 $ (人)
感染していない人9999万人のうちの $ 99990000 \times \frac{1}{100} =999900 $ (人)
よって, 求める条件つき確率は
\[ \frac{9900}{9900+999900}=\frac{1}{102} \hspace{1cm} \cdots \mbox{(答)} \]
(2)方針を正方形で考えると
(1)の結果、無作為に検査をすると陽性となった人の99%が感染していない人になってしまうことがわかりましたが、陽性になった人を再検査するとどうなるのでしょうか?
正方形で考えると、横長の斜線部に該当する人たちは感染しているので、再検査でも99%が陽性になります。
一方、縦長の斜線部に該当する人たちは感染していないので、再検査では1%が陽性になります。
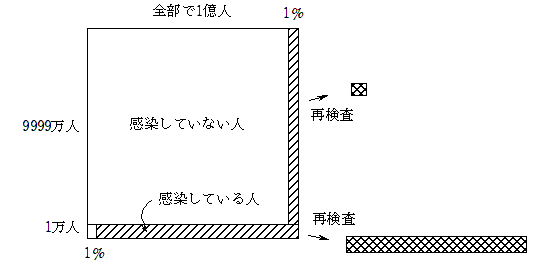
求めるべき条件付き確率は、2つの網目部分を分母に、上の網目部分を分子にすることで計算できます。
(2)解答
2度の検査でどちらも陽性となる確率は
\[ \frac{0.01}{100} \times \frac{99}{100} \times \frac{99}{100}+\frac{99.99}{100} \times \frac{1}{100} \times \frac{1}{100}=\frac{0.99 \times 99 +99.99}{1000000} \]
そのうち、感染していて陽性となっている確率は
\[ \frac{0.01}{100} \times \frac{99}{100} \times \frac{99}{100}= \frac{0.99 \times 99}{1000000} \]
なので、求める条件付き確率は
\[ \frac{\frac{0.99 \times 99}{1000000}}{\frac{0.99 \times 99 +99.99}{1000000}}= \frac{0.99 \times 99}{0.99 \times 99 +99.99}= \frac{0.99}{0.99+1.01} =\frac{99}{200} \cdots \mbox{(答)} \]

コメント