問 $ a>0 $ とするとき、3次関数 $ f(x)=x^3 -3ax^2+2a^2 $ (0≦$x$≦2)に関して、次の問いに答えよ。
(1) $a=1$のとき、$y=f(x)$のグラフを描け。
(2) $f(x)$ の最小値 $m(a)$ を求めよ。
(3) $f(x)$ の最大値 $M(a)$ を求めよ。
使えるようになりたいポイント
【ポイント】最大・最小は、「範囲の端」か「極値(頂点)」にある
【ポイント】極値をもつ3次関数は、8つの長方形にピッタリはまる
【ポイント】増減表は、微分結果の2次関数のグラフをざっくり描いてから
解答・解説
場合分けのきっかけをつかもう
(2) では0≦$x$≦2 の区間内に極小値が存在するか否かで、最小値を与える$x$が変わるので、場合分けが生じます。(3)では、両端点$f(0)$と$f(2)$との大小で場合分けになりますが、3次関数を8つの長方形にピッタリはめることができると、$f(0)=f(3a)$がすぐにわかるので見通し良く解答できます。
答
(1)
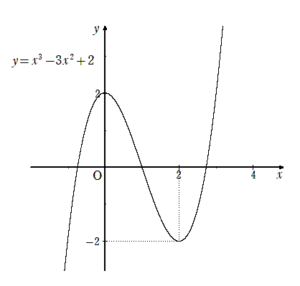
(2)
\begin{eqnarray}
m(a)
=
\begin{cases}
-4a^3+2a^2 & ( 0 < a \leqq 1 \mbox{のとき}) \\ 2a^2-12a+8 & ( 1 \leqq a \mbox{のとき}) \end{cases} \end{eqnarray} (3) \begin{eqnarray} M(a) = \begin{cases} 2a^2-12a+8 & ( 0 < a \leqq \frac{2}{3} \mbox{のとき}) \\ 2a^2 & ( \frac{2}{3} \leqq a \mbox{のとき}) \end{cases} \end{eqnarray}
(1)解答
$ a=1 $ のとき
\[f(x)=x^3-3x^2+2
\]
なので
\begin{eqnarray}
f'(x)& = & 3x^2-6x \\
& = & 3x(x-2)
\end{eqnarray}
増減表は
\begin{array}{c|ccccc}
x & \cdots & 0 & \cdots & 2 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 2 & \searrow & -2 & \nearrow
\end{array}
(2)解答
\begin{eqnarray}
f'(x)& = & 3x^2-6ax \\
& = & 3x(x-2a)
\end{eqnarray}
より、増減表は
\begin{array}{c|ccccc}
x & \cdots & 0 & \cdots & 2a & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 2a^2 & \searrow & -4a^3+2a^2 & \nearrow
\end{array}
となるので、
i) $ 2 \leqq 2a $ すなわち $ 1 \leqq a $ のとき
\[
m(a)=f(2)=2a^2-12a+8
\]
ii) $ 2a \leqq 2 $ すなわち $ 0 < a \leqq 1 $ のとき \[ m(a)=f(2a)=-4a^3+2a^2 \] i), ii) より \begin{eqnarray} m(a) = \begin{cases} -4a^3+2a^2 & ( 0 < a \leqq 1 \mbox{のとき}) \\ 2a^2-12a+8 & ( 1 \leqq a \mbox{のとき}) \end{cases} \end{eqnarray}
(3)解答
$ f(3a)=2a^2=f(0) $ なので
i) $ 2 \leqq 3a $ すなわち $ \frac{2}{3} \leqq a $ のとき
\[ M(a)=f(0)=2a^2 \]
ii) $ 3a \leqq 2 $ すなわち $ 0< a \leqq \frac{2}{3} $ のとき \[ M(a)=f(2)=2a^2-12a+8 \] i), ii) より \begin{eqnarray} M(a) = \begin{cases} 2a^2-12a+8 & ( 0 < a \leqq \frac{2}{3} \mbox{のとき}) \\ 2a^2 & ( \frac{2}{3} \leqq a \mbox{のとき}) \end{cases} \end{eqnarray}

コメント