（１） $3x^2+4xy+y^2-7x-y-6 $
（２） $4x^2+4xy-3y^2+6x+17y-10$
方針は2つ
このタイプの解答方針は、2つ。
ひとつめは、学校でこう習うと思われる方法で、$x$についてまとめる方法【A】。
もう一つは、頭から因数分解する方法【B】。
慣れると、【B】のほうが速いようにも思いますが、どちらでもできるほうが好ましいです。
整数問題のときは積の形をつくることが多く、この場合は頭から因数分解したほうが効率良いです。一方で、2変数関数の最大最小問題になるときは1文字に着目することになるので、$x$か$y$についてまとめることが必須となります。
まず、【A】のほうからやってみます。
（１） $3x^2+4xy+y^2-7x-y-6 $
【解答A】$x$の次数に着目すると \begin{eqnarray} \mbox{与式} &=& 3\color{yellow}{x^2}+4y\color{red}{x}-7\color{red}{x} +y^2-y-6 \\ &=& 3x^2+(4y-7)x+(y-3)(y+2) \\ &=& (x+y-3)(3x+y+2) \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}
続いて、【B】の方法です。全体の次数に着目すると、$x^2, \, xy, \, y^2 $ の項が２次になり、この部分から因数分解できます。
この先はたすき掛け因数分解なら一瞬なのですが、たすきがけが難しい場合は、かっこの中の係数が異なる文字に着目してもう一方をいったん無視します。
ここでは $y$ を無視して $3x^2-7x-6$を因数分解し、そのあと $y$を戻すことで答えが出てきます。解答用紙には書かずに、①のあと結果の式を書いておきましょう。
$3x^2-7x-6$を因数分解すると \begin{eqnarray} &=& \color{yellow}{3}x^2 \color{red}{-7}x\color{yellow}{-6}\\ &=& \color{yellow}{3}x^2+ (\color{red}{-9+2})x\color{yellow}{-6}\\ &=& 3x^2-9x+2x-6 \\ &=& 3x(x-3)+2(x-3) \\ &=& (x-3)(3x+2) \end{eqnarray} あとは $y$を戻して \[ (x+y-3)(3x+y+2) \hspace{5mm}\cdots \mbox{(答)} \] を①のすぐ下の行に書きましょう。
答案に書けるようにするには、①でかっこでくくった部分を両方おきかえます。おきかえても手間がかかりますが、次のようになります。
①で \begin{eqnarray} x+y=A \hspace{5mm}\cdots \mbox{②} \\ 3x+y=B \hspace{5mm}\cdots \mbox{③} \end{eqnarray} とおくと, $\displaystyle\frac{\mbox{③}-\mbox{②}}{2} $より \[x=\frac{B-A}{2} \] $\displaystyle\frac{\mbox{②} \times 3-\mbox{③}}{2} $より \[y=\frac{3A-B}{2} \] なので \begin{eqnarray} \mbox{①} &=& AB-7\cdot \frac{B-A}{2} -\frac{3A-B}{2}-6 \\ &=& AB+2A-3B-6 \\ &=& A(B+2)-3(B+2) \\ &=& (B+2)(A-3) \\ &=& (3x+y+2)(x+y-3) \hspace{5mm}\cdots \mbox{(答)} \end{eqnarray}
続いて、例題(2)です。まず【A】の方法です。
なお、この場合のたすきがけ部分は、定数部分を無視しても$y$を無視してもどちらでも実行できます。 $y$を含む項あるいは定数部分は、あとからくっつけるとOKです。
たすきがけ因数分解が難しいという人は、④のかっこでくくった部分のyのある部分だけを考えて
\begin{eqnarray} 4x^2+4yx-3y^2 &=& 4x^2+6yx-2yx-3y^2 \\ &=& 2x(2x+3y)-y(2x+3y) \\ &=& (2x+3y)(2x-y) \end{eqnarray} の因数分解を答案以外の場所で計算してあと$, \, y$ のところを $y-5,\, 3y$ のところを $3y-2$ に戻した \[ = \{2x+(3y-2)\}\{2x-(y-5)\} \] すなわち \[ = (2x+3y-2)(2x-y+5) \] を④のすぐ下の行に書いて答えとしましょう。続いて、【B】の方法です。
$x$を残した場合は、係数がそろっているので \begin{eqnarray}4x^2+6x-10 &=&4x^2+10x-4x-10 \\ &=& 2x(2x+5)-2(2x+5) \\ &=& (2x+5)(2x-2) \end{eqnarray} のあと、$17y$ が現れるように $3y$ を後ろのかっこに、$-y$ を前のかっこに補って \[ =(2x-y+5)(2x+3y-2)\] を⑤の下に書きましょう。
$y$を残した場合は、マイナスの符号をそのままにして \begin{eqnarray}-3y^2+17y-10 &=&-3y^2+15y+2y-10 \\ &=& -3y(y-5)+2(y-5) \\ &=& (y-5)(-3y+2) \end{eqnarray} のあと、$2x$ をくっつけて \[ =(2x+y-5)(2x-3y+2)\] を⑤の下に書きましょう。
【練習問題】次の式を因数分解せよ。
（１）$ 2x^2-xy-y^2-7x+y+6 $
（２）$ 3x^2+5xy-2y^2-x+5y-2 $
（１）解答
【A】の方法で解くと
\begin{eqnarray} \mbox{与式}&=&2x^2-xy-7x -y^2+y+6 \\ &=&2x^2-(y+7)x -(y^2-y-6) \\ &=&2x^2-(y+7)x -(y-3)(y+2) \\ &=&(2x+y-3)\{x-(y+2)\} \\ &=&(2x+y-3)(x-y-2) \hspace{10mm} \cdots \mbox{(答)} \end{eqnarray}
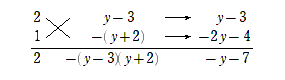
【B】の方法で解くと
$2x^2-xy-y^2=(2x+y)(x-y)$ なので
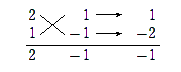
\begin{eqnarray} \mbox{与式}&= &(2x+y)(x-y)-7x+y+6 \\ &=&\{(2x+y)-3\}\{(x-y)-2 \} \\ &=&(2x+y-3)(x-y-2) \hspace{10mm} \cdots \mbox{(答)} \end{eqnarray}
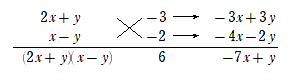
（２）解答
【A】の方法で解くと
\begin{eqnarray} \mbox{与式}&=&3x^2+5xy-x-2y^2+5y-2 \\ &=&3x^2+(5y-1)x-(2y^2-5y+2) \\ &=&3x^2+(5y-1)x-(2y-1)(y-2) \end{eqnarray}
\begin{eqnarray} &=&\{3x-(y-2)\} (x+2y-1) \\ &=&(3x-y+2)(x+2y-1) \hspace{10mm} \cdots \mbox{(答)}\end{eqnarray}
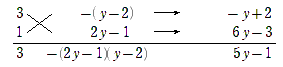
【B】の方法で解くと
$ 3x^2+5xy-2y^2 =(3x-y)(x+2y) $ なので
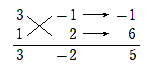
\begin{eqnarray} \mbox{与式}&= &(3x-y)(x+2y)-x+5y-2 \\ &=&\{(3x-y)+2\}\{(x+2y)-1 \} \\ &=&(3x-y+2)(x+2y-1) \hspace{10mm} \cdots \mbox{(答)} \end{eqnarray}
YouTube動画解説
YouTubeでの解説はこちらです。
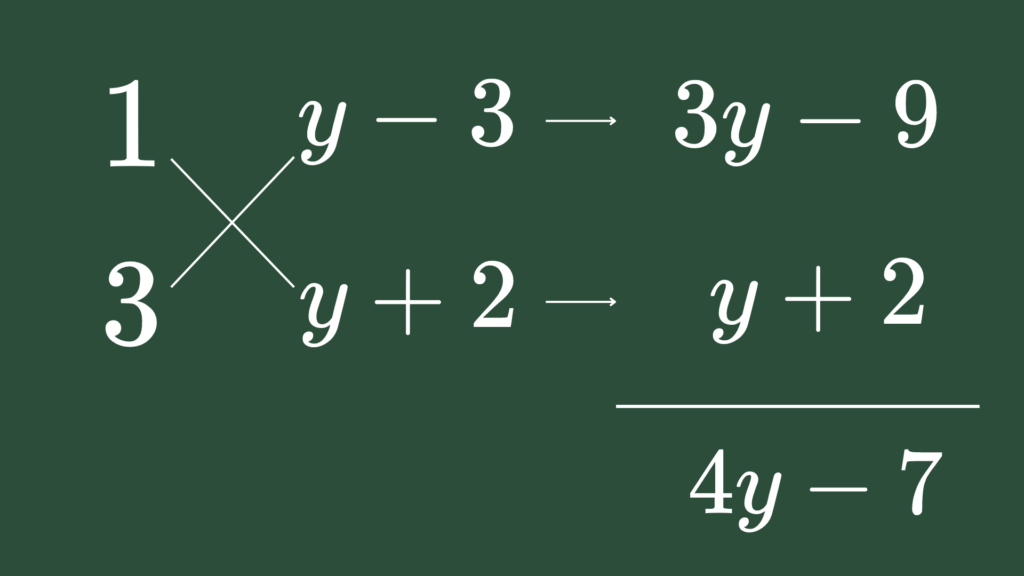
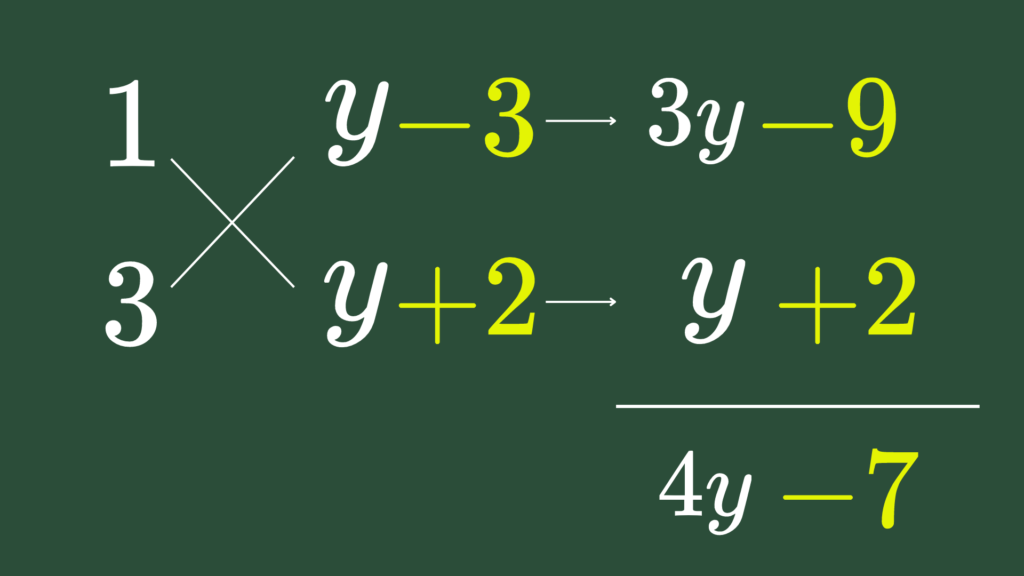
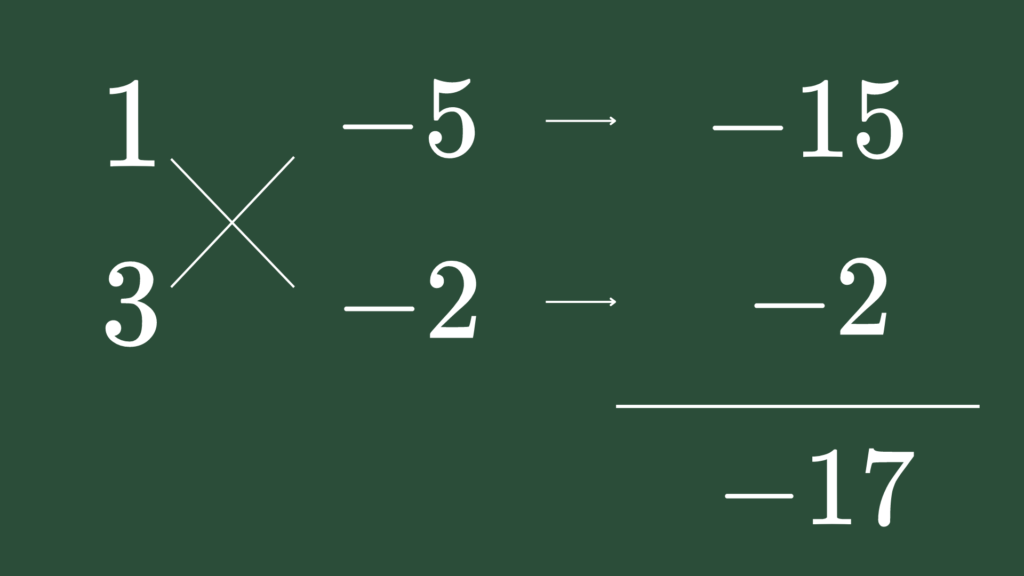
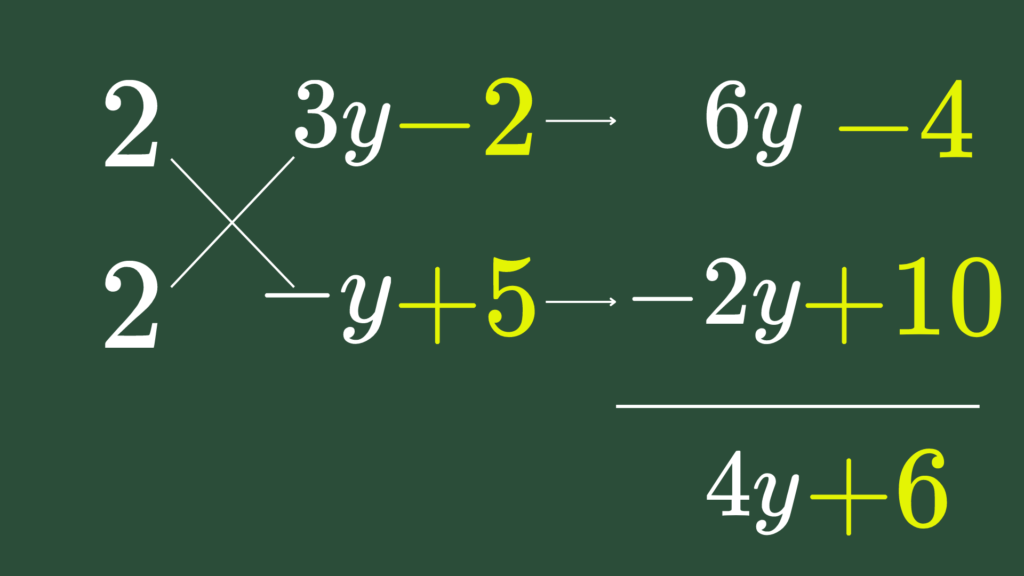
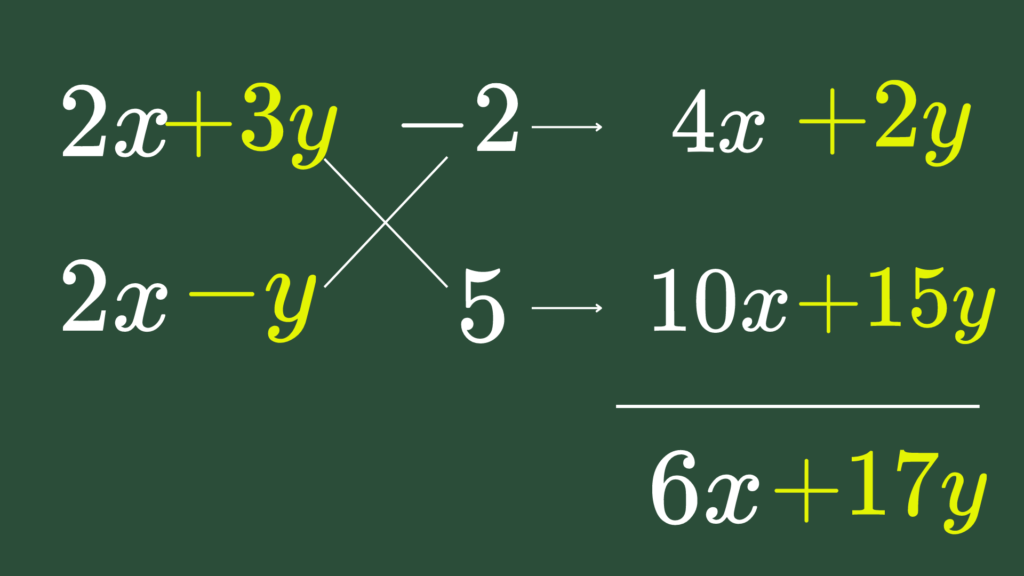
コメント