2次関数が関係する面積のうち、接線がからんだ場合の計算を早く行う練習をしましょう。
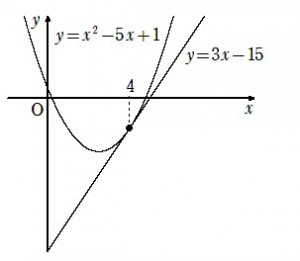
【問題】曲線C: y=x2-5x+1 上の点A(4,-3) における接線をmとする。このとき, 曲線C, 接線mと y軸で囲まれた部分の面積Sを求めよ。
使えるようにしたいチェックポイント
【ポイント1】引き算は後ろを基準に考える
【ポイント2】「x=aで接する」と言われれば「aを重解にもつから(x-a)2の形」に変形できる
【ポイント3】(x-a)2のままで積分する
接線mの方程式を求めて、上側の曲線C から下側の接線m を引いて積分計算ではセンター試験などでは時間が足りなくなります。接点の x 座標が与えられていることに着目すると計算も簡単です。
YouTube解説
答
\[
\frac{64}{3}
\]
【解答】曲線Cと接線mは x=4 である点Aで接していて、曲線Cは下に凸なので
時間がかかってしまいますが、最も一般的と思われる解答をつくってみます。
【別解】f(x)=x2-5x+1 とおくと, f'(x)=2x-5 より f'(4)=3 とから点Aにおける接線の方程式は
すなわち
ここで重要なことは、「結果が同じになって計算できた」ではありません。
赤で記した(1)と(2)の式に着目してください。
並べてみますね
∫とdxの間に挟まれた式は計算すると同じ式(数学っぽく言えば恒等式)です。
計算すると同じですが、式の意味が違います。ここで使える考えかたは引き算は後ろが基準という考えかたです。
(2) は y=3x-5 を基準として y=x2-5x+1 を見ています。
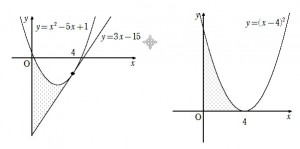
(1) は引き算になっていないのでゼロを補うと y=0 を基準として y=(x-4)2 を見ています。
囲まれた部分の形そのものは違うのですが、面積はまったく同じになります。
面積を求める積分の公式
も「上のf(x)から下のg(x)を引く」というより「下のg(x)を基準にして 上のf(x)を見上げる」ような感覚があるともっと楽しく素早く解けるようになると思います。
x=4で接するf(x)-g(x)=(x-4)2の例をもっと考えよう
この考え方は、数2Bだけでなく非常に応用がひろくいろいろなところで出てきますので、他の例も考えてみましょう。
f(x)-g(x) を計算したら (x-4)2になる、g(x)を基準として見上げると x=4で接しているf(x)のコンビです。
無限にあるので、代表的なものを取り上げていきます。
ここをご覧のあなたは、すぐ下をみないで、是非どんなy=f(x) とy=g(x)があるか紙に書いてみてください。
心の準備はよろしいですか?(おおげさな・・・)
では、3つ f(x)とg(x)のコンビをこれから記します。
まずひとつめは
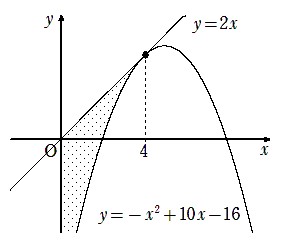
f(x)=2x と g(x)=-x2+10x-16
です。上が直線で下が2次関数です。下の2次関数を基準にして直線を見上げるタイプです。
続いて2つめは
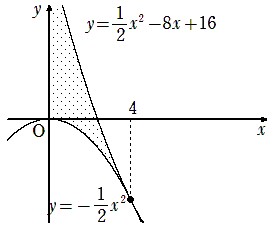
f(x)=1/2x2-8x+16 と g(x)=-1/2x2
です。上も下も2次関数ですが、下の2次関数を基準にして上の2次関数を見上げる感覚をつかめますか?
ここまで、よろしいですか?
では最後の3つめのコンビを発表します。
その前に、再度ここで立ち止まってどんな関数の組合せになるのか、f(x)とg(x)をもう一度考えてみてください。
おまたせしました。では今度こそ3つめのコンビを発表します。
3つめは
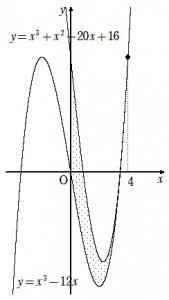
f(x)=x3+x2-20x+16 と g(x)=x3-12x です。最後は3次関数同士ですが引き算すると打消しあいます。
下のg(x)=x3-12xを基準としてf(x)を見上げるとx=4で接する2次関数のように変化しているわけです。
ここまでよろしいでしょうか?
再度まとめると
下側のg(x)を基準にして上側のf(x)をみると、計算に必要なのはf(x)-g(x)の計算結果であり、その計算結果はx軸を基準にして見上げたときの2次関数を扱うことにより簡単に計算ができます。
f(x) と g(x) はどんな式であれ、f(x)-g(x)が同じであれば、すべておなじ面積になります。
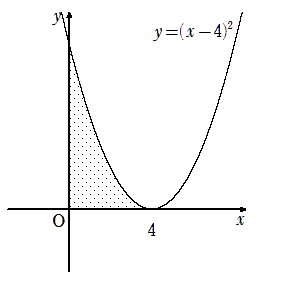
結局、x軸を基準として、x=4 で接している2次関数y=(x-4)2の面積を計算すればよく、あとはカッコを外さずに
を使うだけです。
すこし練習すればすぐに使えるようになります。がんばりましょう!
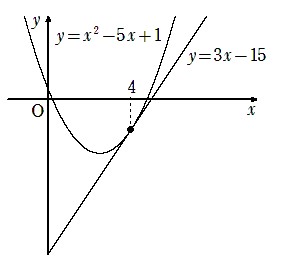
コメント