今回はベクトルと内分・外分についての問題です。内分点の公式を覚えているのは悪いことではないですが、内分・外分の位置さえわかれば公式がなくてもベクトルで表せるようにしたいところです。
問題
△ $OAB$ を含む平面あるいは空間において
(1)$AB$を $2:3$ に内分する点を$P$とするとき,
(a) $ \overrightarrow{AP} $を $ \overrightarrow{AB} $ を用いて表せ。 (b) $ \overrightarrow{OP} $を $ \overrightarrow{OA} $ と $ \overrightarrow{OB} $ を用いて表せ。
(2)$AB$を $3:1$ に外分する点を$Q$とするとき,
(a) $ \overrightarrow{AQ} $を $ \overrightarrow{AB} $ を用いて表せ。 (b) $ \overrightarrow{OQ} $を $ \overrightarrow{OA} $ と $ \overrightarrow{OB} $ を用いて表せ。
(3)2点 $A(1, \ 3), \ B(2, \ -1)$ を通る直線が, $x$ 軸と点 $C$ で交わるとき $AC$ は $AB$ を何対何に内分するか求めよ。
(4)2点 $A(0, \ -3, \ 5), \ B(2, \ 0, \ 4)$ を通る直線が, $xy$ 平面と点 $D$ で交わるとき $AD$ は $AB$ を何対何に外分するか求めよ。
数学のコツ壺
基準となるベクトルをはっきりと
当たり前かもしれないですが、たとえば「平面上の点ならば(平行でなくゼロベクトルでもない)2つのベクトル、一直線上の点ならば1つのベクトルで表せます」が、だからといって必ずしも $ \overrightarrow{OA} $ と $ \overrightarrow{OB} $ で表せばよいというわけでもありません。
たとえ空間のベクトルの問題でも、直線上の2点を結ぶ $ \overrightarrow{AB} $ を基準に考えたほうが簡単な場合もあります。
どこを始点にしたベクトルを基準にすればよいか、基本的な問題から臨機応変に対応できるように練習しましょう。
2つの基準ベクトルは座標に寄せて設定する
平面のベクトルではほとんどの場合, $ \overrightarrow{OA} $ と $ \overrightarrow{OB} $ が基準になりますが, この二つを適当に描くのではなく、直交座標の $xy$ 平面に寄せて描くことがおすすめです。
答えの妥当性のチェックであったり、穴埋めのときにはほとんど一瞬で答えが見つかったりもします。
外分点の公式の証明
外分点は公式以前にどんな場所にあるかを見つけられることが大切です。場所がわかれば分点の公式は不要なくらいですが、いちおう証明しておきます。
下図のように点 $P$ が線分 $AB$ を $ m:n (m>n) $ に外分する場合で, 外分点の公式の証明をしておきます。
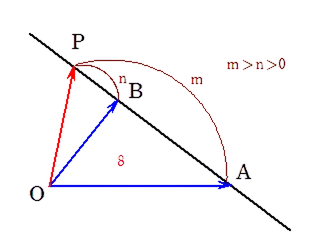
基準となるベクトルを $ \overrightarrow{AB} $ とすれば,
\[ \overrightarrow{AP}=\frac{m}{m-n}\overrightarrow{AB} \hspace{5mm} \cdots {①}\]
なので, この両辺に $\overrightarrow{OA}$ を加えると
\begin{eqnarray}
\mbox{①の左辺} &=& \overrightarrow{OA}+\overrightarrow{AP} \\
&=& \overrightarrow{OP} \\
\mbox{①の右辺} &=& \frac{m}{m-n}\overrightarrow{AB}+\overrightarrow{OA} \\
&=& \frac{m}{m-n}(\overrightarrow{OB}-\overrightarrow{OA})+\overrightarrow{OA} \\ &=& \frac{m}{m-n}(\overrightarrow{OB}-\overrightarrow{OA})+\frac{m-n}{m-n}\overrightarrow{OA} \\
&=& \frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n}
\end{eqnarray}
となるので
\[ \overrightarrow{OP}= \frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n} \]
解答
(1)解答
(1)点 $P$ は $AB$ を $2:3$ に内分するので, 下図のような位置に点 $P$はある。
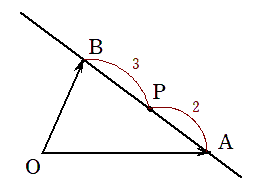
(a) $ \overrightarrow{AP} $を $ \overrightarrow{AB} $ を用いて表すと
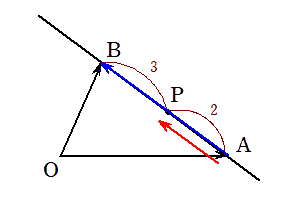
\[ \color{red}{\overrightarrow{AP}} =\frac{2}{5} \color{blue}{\overrightarrow{AB}} \hspace{5mm} \cdots \mbox{①(答)} \]
(b) $ \overrightarrow{OP} $を $ \overrightarrow{OA} $ と $ \overrightarrow{OB} $ を用いて表すと
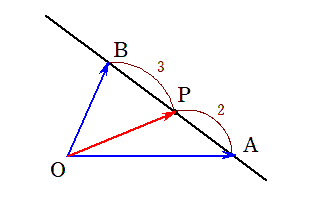
①の両辺に $ \overrightarrow{OA} $ を加えて(2つの青い基準のベクトルに合わせにいくと)
\begin{eqnarray}
\overrightarrow{OA} + \overrightarrow{AP} &=&\frac{2}{5} \overrightarrow{AB} + \color{blue}{\overrightarrow{OA}} \\
\color{red}{\overrightarrow{OP}} &=& \frac{2}{5}(\overrightarrow{AO}+\color{blue}{\overrightarrow{OB}}) + \color{blue}{\overrightarrow{OA}} \\
&=& \frac{2}{5}(-\color{blue}{\overrightarrow{OA}}+\color{blue}{\overrightarrow{OB}}) + \frac{5}{5}\color{blue}{\overrightarrow{OA}} \\
&=& \frac{3}{5}\color{blue}{\overrightarrow{OA}}+\frac{2}{5}\color{blue}{\overrightarrow{OB}} \hspace{5mm} \cdots \mbox{(答)}
\end{eqnarray}
もちろんベクトルの引き算が使える人は, ①から
\[ \overrightarrow{OP}-\overrightarrow{OA}= \frac{2}{5}(\overrightarrow{OB}-\overrightarrow{OA})\]
と変形してかまいません。
ここでは, $O$ をスタートして $A$ を経由して $P$ まで行くイメージで解いてみました。
(2)解説・解答
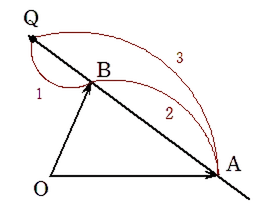
まず $AB$を $3:1$ に外分する点を$Q$ が図形的にどこにあるかを確認しましょう。
外分が苦手な人は 大きい数値を小さい数値と残りに分割しましょう。
ここでは $(2+1):1$と見ます。こうすると $A$ から $2$ 進むと $B$ に到達し, さらに1進むと $Q$ に到達。そのあと1戻って再び $B$ に到達することができます。
(2)解答
$AB$を $3:1$ に外分する点を$Q$ は下図のようになる。
(a) $ \overrightarrow{AR} $を $ \overrightarrow{AB} $ を用いて表すと
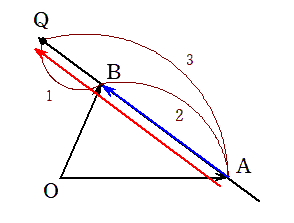
\[ \color{red}{\overrightarrow{AQ}} =\frac{3}{2} \color{blue}{\overrightarrow{AB}} \hspace{5mm} \cdots \mbox{②(答)} \]
(b) $ \overrightarrow{OQ} $を $ \overrightarrow{OA} $ と $ \overrightarrow{OB} $ を用いて表すと
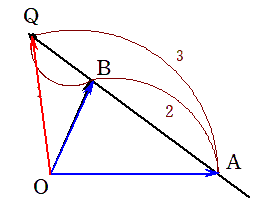
②の両辺に $ \overrightarrow{OA} $ を加えて(2つの青い基準のベクトルに合わせにいくと)
\begin{eqnarray}
\overrightarrow{OA} + \overrightarrow{AQ} &=&\frac{3}{2} \overrightarrow{AB} + \color{blue}{\overrightarrow{OA}} \\
\color{red}{\overrightarrow{OQ}} &=& \frac{3}{2}(\overrightarrow{AO}+\color{blue}{\overrightarrow{OB}}) + \color{blue}{\overrightarrow{OA}} \\
&=& \frac{3}{2}(-\color{blue}{\overrightarrow{OA}}+\color{blue}{\overrightarrow{OB}}) + \frac{2}{2}\color{blue}{\overrightarrow{OA}} \\
&=& -\frac{1}{2}\color{blue}{\overrightarrow{OA}}+\frac{3}{2}\color{blue}{\overrightarrow{OB}} \hspace{5mm} \cdots \mbox{(答)}
\end{eqnarray}

コメント