数Ⅰの展開全パターン

分配法則

\[ a(x + y) = ax + ay 　\] \[ a(x \, -\hspace{1mm} y) = ax \, – \, ay \] カッコが前にあると \[ (a + b) x = ax+bx \] \[ (a \hspace{2mm} – \hspace{1mm} b) x = ax \hspace{1mm} -\hspace{1mm} bx \]

例題

【例題1】 \begin{eqnarray} 3 \times (4 + 5) &=& 3 \times 4 + 3 \times 5 \\ &=& 12 + 15 \\ &=& 27 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題2】 \begin{eqnarray} x(2x \,- 3) &=& x \cdot 2x \,- x \cdot 3 \\ &=& 2x^2 \,- 3x \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題3】 \begin{eqnarray} (5x^2 \,- 4x)y &=& 5x^2 \cdot y \,- 4x \cdot y \\ &=& 5x^2y \,- 4xy \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題4】 \begin{eqnarray} 2x(3xy \,- 5x + 6) &=& 2x \cdot 3xy \,- 2x \cdot 5x + 2x \cdot 6 \\ &=& 6x^2y \,- 10x^2 + 12x \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

2次の展開公式

\begin{eqnarray} (a + b)^2 &=& a^2 + 2ab + b^2 \\ (a \,- b)^2 &=& a^2 \,- 2ab + b^2 \\ (a + b)(a\, – b) &=& a^2 \,- b^2 \\ (x + a)(x+b) &=& x^2 + (a+b)x + ab \\ (ax + b)(cx+d) &=& (a+c)x^2 + (ad+bc)x+bd \\ \end{eqnarray} \begin{align*} (a + b + c)^2 &= a^2 + b^2 + c^2 + 2ab + 2bc + 2ca \end{align*} \begin{eqnarray} (ax + by+c)(dx+ey+f) \hspace{100mm} \\ = adx^2 +(ae+bd)xy +bey^2 +(af+cd)x+(bf+ce)y+cf \end{eqnarray}

• おきかえのコツ

1.おきかえた文字の範囲は？
2.おきかえた文字は元に戻す

$(a+b)^2$の展開公式

\[ (a + b)^2 = (a + b)(a + b) \] となることを、確認しておきましょう。2つの$a+b$ の左側を $X$とおくと \begin{eqnarray} (a + b)^2 &=& X(a + b) \\ &=& Xa+Xb \end{eqnarray} となるが, $\color{yellow}{X=a+b} $ なので \begin{eqnarray} (a + b)^2 &=& \color{yellow}{(a+b)}a+\color{yellow}{(a+b)}b \\ &=& a^2+ba +ab+b^2 \\ &=& a^2+2ab+b^2 \end{eqnarray}

$(a+b)^2$ の展開公式と正方形などの面積の関係

\[ (a + b)^2 = a^2+2ab+b^2 \]

正方形の一辺の長さが$a$から$a+b$に変わると、面積は赤い部分から、青の長方形2つ分と紫の正方形分だけ増えます。$a=20, \ b=5$の場合は

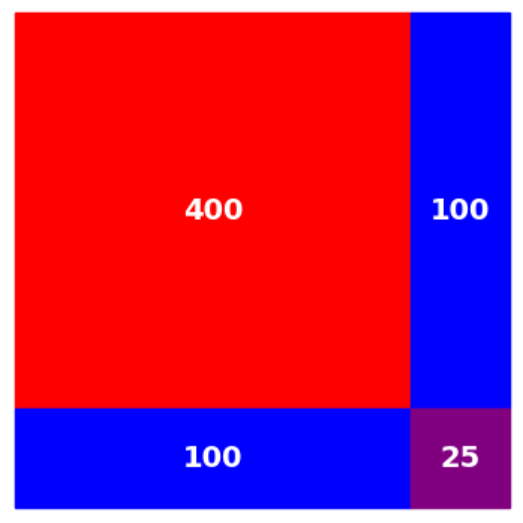
のようになります。

$(a+b)^2, \, (a-b)^2$ の例題

【例題1】$ \hspace{20mm} (x+1)^2 $
【例題2】$ \hspace{20mm} (3+y)^2 $
【例題3】$ \hspace{20mm} (x-5)^2 $
【例題4】$ \hspace{20mm} (2x+3)^2 $
【例題5】$ \hspace{20mm} (x-2y)^2 $

これらの問題を \[ \color{yellow}{(a + b)^2 = a^2 + 2ab + b^2} \] \[ \color{yellow}{(a \,- b)^2 = a^2 \,- 2ab + b^2} \] を使って計算してみましょう。

$(a+b)^2, \, (a-b)^2$ の例題

【例題1】 \begin{eqnarray} (x+1)^2 &=& x^2+2 \cdot x \cdot 1+1^2 \\ &=& x^2+2x+1 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題2】 \begin{eqnarray} (3+y)^2 &=& 3^2 +2 \cdot 3 \cdot y +y^2 \\ &=& y^2+6y+9 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題3】 \begin{eqnarray} (x-5)^2 &=& x^2 -2 \cdot x \cdot 5 + 5^2 \\ &=& x^2 -10x+25 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} あるいは $\{x+(-5)\}^2 $と見ることで \begin{eqnarray} (x-5)^2 &=& \{x+(-5)\}^2 \\ &=& x^2 +2 \cdot x \cdot (-5) + (-5)^2 \\ &=& x^2 -10x+25 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題4】 \begin{eqnarray} (2x+3)^2 &=& (2x)^2+2 \cdot 2x \cdot 3 + 3^2 \\ &=& 4x^2 +12x+9 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題5】 \begin{eqnarray} (x-2y)^2 &=& x^2-2 \cdot x \cdot 2y +(2y)^2 \\ &=& x^2-4xy +4y^2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} あるいは $\{x+(-2y)\}^2 $と見ることで \begin{eqnarray} (x-2y)^2 &=& \{x+(-2y)\}^2 \\ &=& x^2 +2 \cdot x \cdot (-2y) + (-2y)^2 \\ &=& x^2 -4xy+4y^2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

和と差の積$(a+b)(a-b)$タイプの展開公式の証明

\[ (a+b)(a-b) = a^2 -b^2 \] $a+b=X$とおくと \begin{eqnarray} (a+b)(a-b) &=& X(a-b) \\ &=& Xa-Xb \\ \end{eqnarray} となるが, $\color{yellow}{X=a+b} $ なので \begin{eqnarray} &=& (\color{yellow}{a+b})a- (\color{yellow}{a+b})b \\ &=& a^2+ba-(ab+b^2 )\\ &=& a^2-b^2 \end{eqnarray}

$(a+b)(a-b)$ の展開例題

【例題1】$ \hspace{20mm} (x+4)(x-4) $
【例題2】$ \hspace{20mm} (a+6b)(a-6b) $
【例題3】$ \hspace{20mm} (x-3y)(x+3y) $
【例題4】$ \hspace{20mm} (9-x)(9+x) $

これらの問題を \[ \color{yellow}{(a + b)(a-b) = a^2 – b^2} \] を使って計算してみましょう。

$(a+b)(a-b)$ の展開例題

【例題1】 \begin{eqnarray} (x+4)(x-4)&=& x^2-4^2 \\ &=& x^2 – 16 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題2】 \begin{eqnarray} (a+6b)(a-6b)&=& a^2-(6b)^2 \\ &=& a^2 – 36b^2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題3】 \begin{eqnarray} (x-3y)(x+3y)&=& x^2-(3y)^2 \\ &=& x^2 – 9y^2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}【例題4】 \begin{eqnarray} (9-x)(9+x)&=& 9^2-x^2 \\ &=& -x^2 + 81 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

$(x+a)(x+b)$の展開公式の証明

\[ (x + a)(x+b) = x^2 + (a+b)x + ab \] $x+b=X$とおくと \begin{eqnarray} (x + a)(x+b) &= (x + a)X \\ &= xX+aX \\ \end{eqnarray} となるが, $\color{yellow}{X=x+b} $ なので \begin{eqnarray} &= x\color{yellow}{(x+b)}+a\color{yellow}{(x+b)} \\ &= x^2+bx+ax+ab \\ &= x^2+(a+b)x+ab \end{eqnarray} $ax$ と $bx$ はどちらも $x$が一つだけついてる「$x$1次の項」なので、同類項をまとめました。

• 展開はカッコの中から1つずつ選んで掛ける

(x+a)(x+b) のカッコの中から1つずつ選んで掛けると

\[ (x + a)(x+b) \]

前のカッコの中からは $x$ か $a,$ 後ろのカッコの中からは $x$ か $b$ を選んで掛けると、2通りずつなので全部で4つ(4項)現れます。

前からも後ろからも $x$ を選んで掛けると $x^2$ が出ます。

これが $x2$ 次の項です。続いて $x$ 1次の項を探して行きます。

前のカッコの中からは $x,$ 後ろのカッコの中からは $b$ を選んで掛けると $bx$ が出ます。前のカッコの中から $a,$ 後ろのカッコの中からは $x$ を選んで掛けると $ax$ が出ます。

これで $x1$次の項が出たので、最後に $x$のない部分として、前のカッコの中から $a,$ 後ろのカッコの中から $b$ を選んで掛けて全部足すと

\[ x^2+(a+b)x+ab \]

となります。

$(x+a)(x+b)=x^2+(a+b)x+ab$と長方形の面積の関係

\[ (x + a)(x+b) = x^2 + (a+b)x + ab \]

正方形の一辺の長さが$x$から$x+a$と$x+b$ に変わると、面積は赤い部分から、青の長方形2つ分と紫の長方形分だけ増えます。$x=10, \, a=5, \, b=3$ の場合は

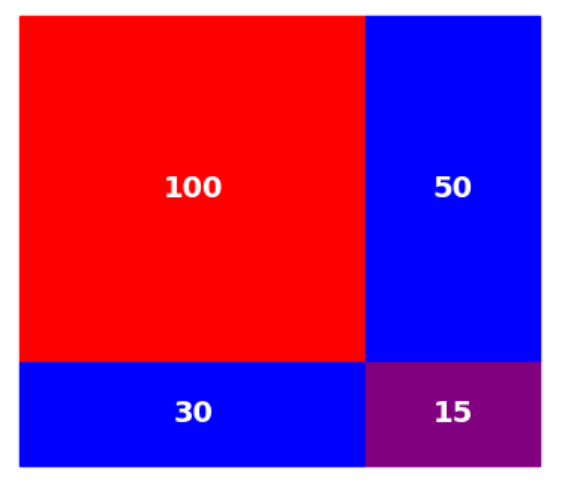
のようになります。

$(x+a)(x+b)=x^2+(a+b)x+ab$ を縦書きの掛け算で

\begin{array}{r} x \hspace{3mm} + \hspace{3mm}a \\ \times ) \hspace{15mm} x \hspace{3mm} + \hspace{3mm} b \\ \hline \hspace{3mm} bx \hspace{1mm} +ab \\ x^2 \hspace{5mm} + \hspace{5mm} ax \hspace{14mm} \\ \hline x^2 + (a+b)x + ab \end{array}

• 対称式

文字を入れ替えたときに、元の式とまったく同じになる式を対称式といいます。
2文字 ($a, \,b$) のときは 和 $a+b$ と積$ab$ だけで、3文字 ($a, \,b, \, c$) のときは 和 $a+b+c$ と積 $abc$ と積和 $ab+bc+ca$ だけで式を表せます。

$ (x+a)(x+b) $ は、$a$ と $b$ を入れ替えると \[ (x+\color{yellow}{b})(x+\color{yellow}{a}) \] となり、元の式と同じなので $a, \, b $ に関して対称式です。

$x $ 以外の$a, \, b$は、和 $\color{yellow}{a+b} $ と積 $\color{yellow}{ab}$ だけを使って \[(x+a)(x+b)=x^2+(\color{yellow}{a+b})x+\color{yellow}{ab} \] と表せます。

$x$ と $a$ に関しては、対称式ではありません。

$ (x+a)(x+b) $ で、$x$ と $a$ を入れ替えると \[ (\color{yellow}{a}+\color{yellow}{x})(\color{yellow}{a}+b) \] となり、元の式とは同じではなくなります。

$(x+a)(x+b)$ の展開例題

【例題1】$ \hspace{20mm} (x+1)(x+4) $
【例題2】$ \hspace{20mm} (x+2y)(x+7y) $
【例題3】$ \hspace{20mm} (x-5)(x+3) $
【例題4】$ \hspace{20mm} (a+3b)(a-6b) $

これらの問題を \[ \color{yellow}{(x+a)(x+b) = x^2 + (a+b)x + ab} \] を使って計算してみましょう。

$(x+a)(x+b)$ の展開例題

【例題1】 \begin{eqnarray} (x+1)(x+4) &=& x^2+(1+4)x + 1 \cdot 4 \\ &=& x^2+5x+4 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題2】 \begin{eqnarray} (x+2y)(x+7y) &=& x^2+(2y+7y)x +2y \cdot 7y \\ &=& x^2+9xy+14y^2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題3】 \begin{eqnarray} (x-5)(x+3) &=& x^2 +(-5+3)x + (-5) \cdot 3 \\ &=& x^2 -2x-15 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題4】 \begin{eqnarray} (a+3b)(a-6b) &=& a^2+(3b-6b)a + 3b \cdot (-6b) \\ &=& a^2 -3ab-18b^2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

たすき掛けタイプ

\[ (ax + b)(cx+d) = (a+c)x^2 + (ad+bc)x+bd \]

この展開式は、逆向きの因数分解で重要です。

おきかえによる証明

$ax+b=X$とおくと \begin{eqnarray} (ax + b)(cx+d) &=& X(cx + d) \\ &=& X \cdot cx+Xd \end{eqnarray} となるが, $\color{yellow}{X=ax+b} $ なので \begin{eqnarray} (ax + b)(cx+d) &=& \color{yellow}{(ax+b)}cx+\color{yellow}{(ax+b)}d \\ &=& ax \cdot cx +b \cdot cx+ax \cdot d+bd \\ &=& acx^2 +(bc+ad)x+bd \end{eqnarray}

$(ax+b)(cx+d)$の展開公式と長方形の面積

\[ (ax + b)(cx+d) = acx^2+(bc+ad)x+bd \]

縦・横の長さが$ax$と$cx$の長方形が、縦に$b,$ 横に$d$ だけ大きくなると、面積は赤い部分から、青の長方形2つ分と紫の長方形分だけ増えます。$a=2, \ b=5, \, c=3, \, d=7, \, x=10 $の場合は

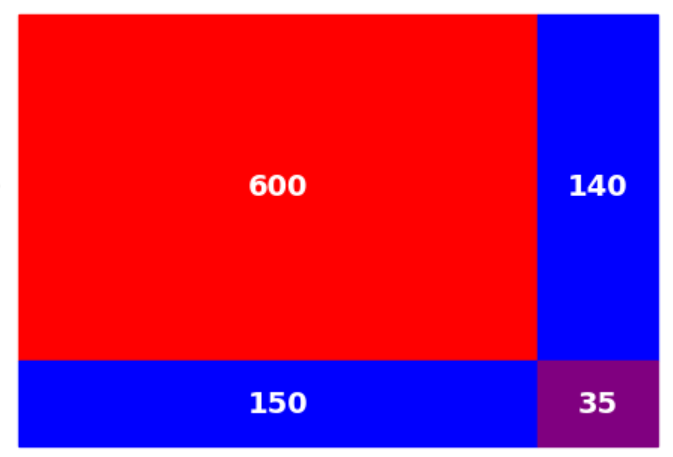
のようになります。

$(ax+b)(cx+d)=acx^2+(ad+bc)x+bd $を縦書きの掛け算で

\begin{array}{r} ax \hspace{3mm} + \hspace{3mm}b \\ \times ) \hspace{15mm} cx \hspace{3mm} + \hspace{3mm} d \\ \hline \hspace{3mm} adx \hspace{1mm} +bd \\ acx^2 \hspace{5mm} + \hspace{5mm} bcx \hspace{14mm} \\ \hline acx^2 + (ad+bc)x + bd \end{array}

たすき掛けタイプ $(ax+b)(cx+d)$ の展開例題

【例題1】$ \hspace{20mm} (2x+3)(x+5) $
【例題2】$ \hspace{20mm} (3x-4)(2x-1) $
【例題3】$ \hspace{20mm} (x+y)(4x+5y) $
【例題4】$ \hspace{20mm} (5x+2)(x-3) $

これらの問題を \[ \color{yellow}{(ax+b)(cx+d) = acx^2 + (ad+bc)x + bd} \] を使って計算してみましょう。

たすき掛け $(ax+b)(cx+d)$ の展開例題

【例題1】 \begin{eqnarray} (2x+3)(x+5) &=& 2x^2 + (2 \cdot 5+3)x + 15 \\ &=& 2x^2 + 13x + 15 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題2】 \begin{eqnarray} (3x-4)(2x-1) &=& 6x^2 +\{ -3 + (-4) \cdot 2\}x + 4 \\ &=& 6x^2 – 11x + 4 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題3】 \begin{eqnarray} (x+y)(4x+5y) &=& 4x^2 + (5y + 4y)x + y \cdot 5y \\ &=& 4x^2 + 9xy + 5y^2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題4】 \begin{eqnarray} (5x+2)(x-3) &=& 5x^2 +\{5 \cdot (-3) +2 \} x – 6 \\ &=& 5x^2 – 13x – 6 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

3項の2乗タイプ

\[ (a + b+c)^2 = a^2 +b^2+c^2 +2ab+2bc+2ca \]

3文字の対称式です。$a$と$b$を入れ替えても、$b$と$c$を入れ替えても、もちろん $c$と$a$を入れ替えても、元の式と同じです。

おきかえによる証明(Ⅰ)

$a+b=X$とおくと \begin{eqnarray} (a + b+c)^2 &=& (X+c)^2 \\ &=& X^2+2cX+c^2 \end{eqnarray} となるが, $\color{yellow}{X=a+b} $ なので \begin{eqnarray} (a + b+c)^2 &=& (\color{yellow}{a+b})^2+2c(\color{yellow}{a+b})+c^2 \\ &=& a^2+2ab+b^2 +2ca+2cb +c^2 \\ &=& a^2+b^2+c^2+2ab+2bc+2ca \end{eqnarray}

おきかえによる証明(Ⅱ)

$a+b+c=X$とおくと \begin{eqnarray} (a + b+c)^2 &=& X(a+b+c) \\ &=& Xa+Xb+Xc \end{eqnarray} となるが, $\color{yellow}{X=a+b+c} $ なので \begin{eqnarray} (a + b+c)^2 &=& (\color{yellow}{a+b+c})a+(\color{yellow}{a+b+c})b+(\color{yellow}{a+b+c})c \\ &=& a^2+ba+ca +ab+b^2+cb +ac+bc+c^2 \\ &=& a^2+b^2+c^2+2ab+2bc+2ca \end{eqnarray}

$(a+b+c)^2$ の展開を縦書きの掛け算で

\begin{array}{r} a \hspace{3mm} + \hspace{3mm}b \hspace{3mm} + \hspace{3mm}c \\ \times ) \hspace{15mm} a \hspace{3mm} + \hspace{3mm} b \hspace{3mm} + \hspace{3mm}c \\ \hline \hspace{3mm} ac \hspace{1mm} +bc \hspace{2mm} + \hspace{1mm} c^2 \\ ab \hspace{2mm} + \hspace{2mm} b^2 \hspace{1mm} + \hspace{1mm} bc \hspace{14mm} \\ a^2 \hspace{2mm} + \hspace{2mm} ab \hspace{1mm} + \hspace{2mm} ac \hspace{27mm} \\ \hline a^2 + b^2 +2ab +2ac +2bc +c^2 \end{array}

$(a+b+c)^2$ の展開例題

【例題1】$ \hspace{20mm} (x+y+3)^2 $
【例題2】$ \hspace{20mm} (3x+2y+z)^2 $
【例題3】$ \hspace{20mm} (x-y+4z)^2 $
【例題4】$ \hspace{20mm} (2x-y-5)^2 $

これらの問題を \[ \color{yellow}{(a+b+c)^2 = a^2 +b^2+c^2+2ab+2bc+2ca} \] を使って計算してみましょう。

$(a+b+c)^2$ の展開例題

【例題1】 \begin{eqnarray} (x+y+3)^2 &=& x^2+y^2+3^2 +2xy+2y \cdot 3+2 \cdot 3 \cdot x \\ &=& x^2+2xy+ y^2+6x+6y+9 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題2】 \begin{eqnarray} (3x+2y+z)^2 &=& (3x)^2+(2y)^2+z^2+2 \cdot 3x \cdot 2y + 2 \cdot 2y \cdot z + 2 \cdot z \cdot 3x \\ &=& 9x^2+4y^2+z^2+12xy+4yz+6zx \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題3】 \begin{eqnarray} (x-y+4z)^2 &=& x^2+(-y)^2+(4z)^2+2 \cdot x \cdot (-y) + 2 \cdot (-y) \cdot 4z + 2 \cdot 4z \cdot x \\ &=& x^2 + y^2 + 16z^2 -2xy-8yz +8zx \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray} 【例題4】 \begin{eqnarray} (2x-y-5)^2 &=& (2x)^2+(-y)^2+(-5)^2+2 \cdot 2x \cdot (-y) + 2 \cdot (-y) \cdot (-5) + 2 \cdot (-5) \cdot 2x \\ &=& 4x^2 – 4xy +y^2 – 20x +10y +25 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

3項の積タイプ

\begin{eqnarray} (ax + by+c)(dx+ey+f) \hspace{100mm} \\ = adx^2 +(ae+bd)xy +bey^2 +(af+cd)x+(bf+ce)y+cf \end{eqnarray}

公式ではありませんが、いずれは因数分解で出てきます。

「$x$と$y$の次数の同じ部分」をおきかえるか、$by+c, ey+f$ を「$y$の1次式」と見ておきかえるかで計算してみましょう($ax+by+c$をおきかえてもできます)。

次数の同じ部分をおきかえると

\begin{eqnarray} (ax + by+c)(dx+ey+f) \hspace{100mm} \\ = adx^2 +(ae+bd)xy +bey^2 +(af+cd)x+(bf+ce)y+cf \end{eqnarray} $ax+by=X, \, dx+ey=Y$とおくと \begin{eqnarray} \mbox{左辺} &=& (X+c)(Y+f) \\ &=& XY+fX+cY+cf \end{eqnarray} となるが, $\color{yellow}{X=ax+by}, \, \color{yellow}{Y=dx+ey} $ なので \begin{eqnarray} \mbox{左辺} &=& (\color{yellow}{ax+by})(\color{yellow}{dx+ey})+f \cdot ( \color{yellow}{ax+by} )+c \cdot ( \color{yellow}{dx+ey} ) +cf \\ &=& adx^2+(ae+bd)xy+bey^2+afx+bfy+cdx+cey+cf \\ &=&adx^2 +(ae+bd)xy +bey^2 +(af+cd)x+(bf+ce)y+cf \end{eqnarray}

「$y$の1次式」をおきかえると

\begin{eqnarray} (ax + by+c)(dx+ey+f) \hspace{100mm} \\ = adx^2 +(ae+bd)xy +bey^2 +(af+cd)x+(bf+ce)y+cf \end{eqnarray} $by+c=X, \, ey+f=Y$とおくと \begin{eqnarray} \mbox{左辺} &=& (ax+X)(dx+Y) \\ &=& adx^2+(aY+dX)x+XY \end{eqnarray} となるが, $\color{yellow}{X=by+c}, \, \color{yellow}{Y=ey+f} $ なので \begin{eqnarray} \mbox{左辺} &=& adx^2+\{a(\color{yellow}{ey+f})+d(\color{yellow}{by+c})\}x+(\color{yellow}{ey+f})(\color{yellow}{by+c}) \\ &=& adx^2+(aey+af+bdy+cd)x+bey^2+(ce+bf)y+cf \\ &=&adx^2 +(ae+bd)xy +bey^2 +(af+cd)x+(bf+ce)y+cf \end{eqnarray}

$(ax + by+c)(dx+ey+f)$ の展開例題

【例題1】$ \hspace{20mm} (2x+y+3)(x+3y-2) $
【例題2】$ \hspace{20mm} (x-2y+1)(2x+3y-2) $

これらの問題を \begin{eqnarray} \color{yellow}{(ax + by+c)(dx+ey+f)} \hspace{100mm} \\ \color{yellow}{= adx^2 +(ae+bd)xy +bey^2 +(af+cd)x+(bf+ce)y+cf } \end{eqnarray} を使って計算してみましょう。

$(ax + by+c)(dx+ey+f)$ の展開例題

【例題1】$(2x+y+3)(x+3y-2)$
$2x+y=X, \, x+3y=Y$とおくと \begin{eqnarray} \mbox{与式} &=& (X+3)(Y-2) \\ &=& XY-2X+3Y-6 \end{eqnarray} となるが, $\color{yellow}{X=2x+y}, \, \color{yellow}{Y=x+3y} $ なので \begin{eqnarray} \mbox{与式} &=& (\color{yellow}{2x+y})(\color{yellow}{x+3y})-2(\color{yellow}{2x+y})+3(\color{yellow}{x+3y})-6 \\ &=& 2x^2+7xy+3y^2-4x-2y+3x+9y-6 \\ &=& 2x^2+7xy+3y^2-x+7y-6 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

$(ax + by+c)(dx+ey+f)$ の展開例題

【例題1別解】$(2x+y+3)(x+3y-2)$
$y+3=X, \, 3y-2=Y$とおくと \begin{eqnarray} \mbox{与式} &=& (2x+X)(x+Y) \\ &=& 2x^2+(2Y+X)x+XY \end{eqnarray} となるが, $\color{yellow}{X=y+3}, \, \color{yellow}{Y=3y-2} $ なので \begin{eqnarray} \mbox{与式} &=& 2x^2+\{ 2(\color{yellow}{3y-2})+(\color{yellow}{y+3}) \} x + (\color{yellow}{3y-2})(\color{yellow}{y+3}) \\ &=& 2x^2+(6y-4+y+3)x+3y^2+7y-6 \\ &=& 2x^2+7xy+3y^2-x+7y-6 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

$(ax + by+c)(dx+ey+f)$ の展開例題

【例題2】$(x-2y+1)(2x+3y-2)$
$x-2y=X, \, 2x+3y=Y$とおくと \begin{eqnarray} \mbox{与式} &=& (X+1)(Y-2) \\ &=& XY-2X+Y-2 \end{eqnarray} となるが, $\color{yellow}{X=x-2y}, \, \color{yellow}{Y=2x+3y} $ なので \begin{eqnarray} \mbox{与式} &=& (\color{yellow}{x-2y})(\color{yellow}{2x+3y})-2(\color{yellow}{x-2y})+(\color{yellow}{2x+3y})-2 \\ &=& 2x^2-xy-6y^2-2x+4y+2x+3y-2 \\ &=& 2x^2-xy-6y^2+7y-2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}

$(ax + by+c)(dx+ey+f)$ の展開例題

【例題2別解】 \[(x-2y+1)(2x+3y-2)=\{x-(2y-1) \}(2x+3y-2) \]なので、
$2y-1=X, \, 3y-2=Y$とおくと \begin{eqnarray} \mbox{与式} &=& (x-X)(2x+Y) \\ &=& 2x^2+(Y-2X)x-XY \end{eqnarray} となるが, $\color{yellow}{X=2y-1}, \, \color{yellow}{Y=3y-2} $ なので \begin{eqnarray} \mbox{与式} &=& 2x^2+\{ (\color{yellow}{3y-2})-2(\color{yellow}{2y-1}) \} x – (\color{yellow}{2y-1})(\color{yellow}{3y-2}) \\ &=& 2x^2+(3y-2-4y+2)x-(6y^2-7y+2) \\ &=& 2x^2-xy-6y^2+7y-2 \hspace{5mm} \cdots (\mbox{答}) \end{eqnarray}