今回の解法のコツ壺は、引き算と割り算の見方についてです。
たし算・掛け算と違い、どちらも順番を変えることができませんが、後ろや分母から見たときの意味を捉えられると、スッと視界が開くことが少なくありません。
引き算の見方「引き算はマイナスの後ろが基準」
$y-b=m(x-a)$ は点$(a, b)$を基準に描いた傾き$m$の直線
直線 $y-b=m(x-a)$ は, 点$(a, b)$から見た直線と考えることができます。
まず基準として, 点$(a, b)$をとり, そこから傾き $m$ の直線を引く感じ。
$y$切片が与えられた $y=mx+n$ も $y-n=m(x-0)$ と変形すると, 点$(0, n)$をとり, そこから傾き $m$ の直線を引くことになります。
接線の公式も $y-f(a)=f'(a)(x-a)$ と左辺に $f(a)$ を残すと, 接点$(a, f(a))$から直線を引くイメージを捉えやすいのでは?
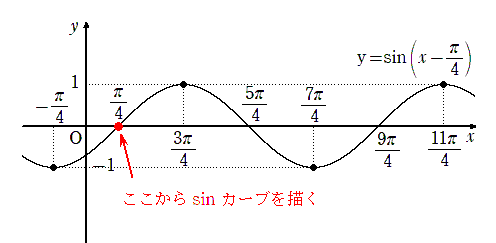
$y=\sin (x -\alpha) $は点$( \alpha , 0)$ を基準としたサインカーブ
曲線 $y=\sin (x -\frac{\pi}{4}) $ は, 点$(\frac{\pi}{4}, 0)$から見たサインカーブと考えることができます。
基準として点$(\frac{\pi}{4}, 0)$ をとり, そこからサインカーブを描くことができます。

コメント